Polynomial 3D Green coordinates and their derivatives for linear cages
IF 2.8
4区 计算机科学
Q2 COMPUTER SCIENCE, SOFTWARE ENGINEERING
引用次数: 0
Abstract
We derive closed-form expressions for polynomial Green coordinates and their derivatives for 3D linear cages. The keys to our derivation are the integrals of polynomials divided by Euclidean distance over a triangle and their derivatives. We demonstrate the usefulness of our polynomial 3D Green coordinates and derivatives on cage-based and variational shape deformations. In cage-based deformation, the coordinates enable deformation from linear polygons of the input cage to polynomial surfaces of any order, allowing users to perform intuitive deformations with a small number of input parameters. In variational deformation, the coordinates and derivatives form a smooth deformation subspace, allowing for the realization of nonlinear shape optimization.
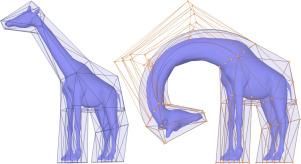
线性笼的多项式三维格林坐标及其导数
我们导出了三维线性笼的多项式格林坐标及其导数的封闭表达式。我们推导的关键是多项式的积分除以三角形上的欧几里得距离和它们的导数。我们证明了我们的多项式三维绿色坐标和导数对基于笼形和变分形状变形的有用性。在基于笼子的变形中,这些坐标可以使输入笼子的线性多边形变形为任何顺序的多项式曲面,允许用户使用少量的输入参数进行直观的变形。在变分变形中,坐标和导数形成光滑的变形子空间,可以实现非线性形状优化。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Computers & Graphics-Uk
工程技术-计算机:软件工程
CiteScore
5.30
自引率
12.00%
发文量
173
审稿时长
38 days
期刊介绍:
Computers & Graphics is dedicated to disseminate information on research and applications of computer graphics (CG) techniques. The journal encourages articles on:
1. Research and applications of interactive computer graphics. We are particularly interested in novel interaction techniques and applications of CG to problem domains.
2. State-of-the-art papers on late-breaking, cutting-edge research on CG.
3. Information on innovative uses of graphics principles and technologies.
4. Tutorial papers on both teaching CG principles and innovative uses of CG in education.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


