Towards a robust time-accurate anisotropically adaptive hybridized discontinuous Galerkin method
IF 3
3区 工程技术
Q3 COMPUTER SCIENCE, INTERDISCIPLINARY APPLICATIONS
引用次数: 0
Abstract
Metric-based anisotropic mesh adaptation has proven effective for the solution of both steady and unsteady problems in terms of reduced computational time and accuracy gain. Especially for time-dependent problems, its generalization to implicit high-order space and time discretizations is, nevertheless, still a challenging task as it requires great care to preserve consistency and stability of the numerical solution. In this regard, the objective of the present work is two-fold. First, we devise an accurate unsteady mesh adaptation algorithm, and second, we introduce a new solution transfer between anisotropic meshes, which preserves the local minima and maxima. Our findings are based on a hybridized discontinuous Galerkin (HDG) solver with diagonally implicit Runge–Kutta (DIRK) time integration, whereas the main focus is on problems for two-dimensional Euler equations including moving shocks.
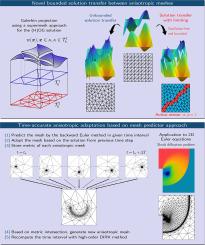
一种鲁棒时准各向异性自适应杂化不连续伽辽金方法
基于度量的各向异性网格自适应在减少计算时间和精度增益方面对解决稳态和非稳态问题都是有效的。特别是对于时变问题,将其推广到隐式高阶空间和时间离散化仍然是一项具有挑战性的任务,因为它需要非常小心地保持数值解的一致性和稳定性。在这方面,目前工作的目标是双重的。首先,我们设计了一种精确的非定常网格自适应算法;其次,我们引入了一种新的各向异性网格之间的解转换方法,该方法保留了局部极小值和最大值。我们的研究结果是基于具有对角隐式龙格-库塔(DIRK)时间积分的杂交不连续伽辽金(HDG)求解器,而主要关注的是包括运动冲击在内的二维欧拉方程的问题。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Computers & Fluids
物理-计算机:跨学科应用
CiteScore
5.30
自引率
7.10%
发文量
242
审稿时长
10.8 months
期刊介绍:
Computers & Fluids is multidisciplinary. The term ''fluid'' is interpreted in the broadest sense. Hydro- and aerodynamics, high-speed and physical gas dynamics, turbulence and flow stability, multiphase flow, rheology, tribology and fluid-structure interaction are all of interest, provided that computer technique plays a significant role in the associated studies or design methodology.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


