Bridging experiments and models, towards a new paradigm: DROP-PINN, a physics-informed neural network to predict droplet rupture in multiphase systems

Abstract

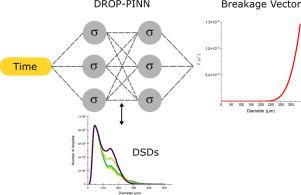
The population balance equation (PBE) is today a convenient tool to describe the evolution of multiphase systems, such as bubble plumes or columns, mixing tanks, solvent extraction columns, where they are used to infer the particle size distribution required to quantify buoyancy forces or the interfacial exchange area. However, the PBE often rely on semi-empirical models (or kernels) to predict the events likely to modify the population properties, such as breakage and coalescence. These kernels contain parameters that are tailored to specific fluid properties and operating conditions, thus limiting their general applicability (i.e. transposition to other operating conditions or processes than those used during model development). As a consequence, accurately predicting the frequency of events that modify the population of droplets remains challenging. In this study, we focus on the breakage phenomenon. Recent advances in machine learning, particularly Artificial Neural Networks (ANNs), present new opportunities for predicting the breakage frequencies. However, ANN training requires a large and high-fidelity dataset, making it time-consuming and error-prone. Physics-Informed Neural Networks (PINNs) may address this challenge by embedding physical laws into the learning process, ensuring physically consistent PBE predictions. This paper introduces a novel PINN-based algorithm that is trained to infer the droplet breakage frequencies in a turbulent agitated vessel without prior knowledge of the breakage kernel. It uses only the PBE discretized structure and a reasonable number of measured droplet size distributions obtained by in situ imaging. The methodology, we have named DROP-PINN, is first deployed and evaluated through controlled simulations, then experimentally over a wide range of dispersed phase viscosity, interfacial tension and agitation speed.