Entanglement and the density matrix renormalization group in the generalized Landau paradigm

Abstract

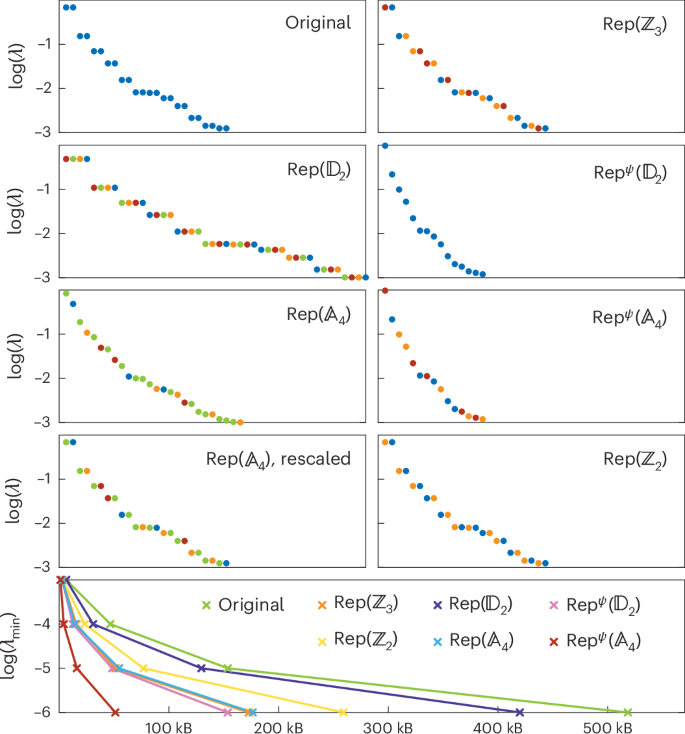
The fields of entanglement theory and tensor networks have recently emerged as central tools for characterizing quantum phases of matter. Here we determine the entanglement structure of ground states of gapped symmetric quantum lattice models and use this to obtain the most efficient tensor network representation of those ground states. We do this by showing that degeneracies in the entanglement spectrum arise through a duality transformation of the original model to the unique dual model where the entire dual symmetry is spontaneously broken. Physically, this duality transformation amounts to a—potentially twisted—gauging of the unbroken symmetry in the original ground state. In general, the dual symmetries of the resulting models are generalized non-invertible symmetries that cannot be described by groups. This result has strong implications for the complexity of simulating many-body systems using variational tensor network methods. For every phase in the phase diagram, the dual representation of the ground state that completely breaks the symmetry minimizes both the entanglement entropy and the required number of variational parameters. We demonstrate the applicability of this idea by developing a generalized density matrix renormalization group algorithm that works on constrained Hilbert spaces and quantify the computational gains obtained over traditional tensor network methods in a perturbed Heisenberg model. Our work testifies to the usefulness of generalized non-invertible symmetries and their formal category theoretic description for the practical simulation of strongly correlated systems.