Elastic guided waves in a spiral wire rope: Theory and modeling
IF 4.2
2区 工程技术
Q1 MECHANICS
引用次数: 0
Abstract
Elastic guided waves are of great interest for the non-destructive evaluation of cables. However, accurately modeling wave propagation in these structures requires complex numerical models that account for their helical, multi-wire geometry and the effects of prestress due to high tension loads. This paper provides a theoretical and computational framework for studying wave propagation in spiral ropes, also known as spiral strands, consisting of a central wire surrounded by two layers of helical wires. These layers are typically wound in opposite directions, breaking continuous symmetry and introducing both line and point interwire contacts. Using a non-trivial curvilinear coordinate system, termed bi-helical, this paper establishes the existence of wave modes in such structures, defines the three-dimensional repetitive unit cell of the spiral rope, and implements a specific Bloch–Floquet wave finite-element method to solve the wave propagation eigenproblem along bi-directional helical coordinates. Interwire contact areas and their dependence on tensile loads are approximated through geometric interpenetrations governed by Hertzian contact laws. The proposed method is validated through numerical experiments on reference test cases, including a cylinder, a seven-wire strand, and a special spiral strand exhibiting translational symmetry. Finally, dispersion curves are presented for various two-layered spiral strands, considering different helix angles and tensile loads. The results reveal complex wave behavior, characterized by multiple veerings strongly influenced by contact areas, paving the way for future experiments and practical applications in the non-destructive evaluation of cables.
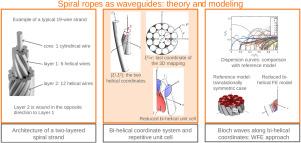
螺旋钢丝绳中的弹性导波:理论与模型
弹性导波对索的无损评价具有重要意义。然而,准确地模拟波在这些结构中的传播需要复杂的数值模型,考虑到它们的螺旋、多线几何形状和由于高张力载荷引起的预应力的影响。本文提供了一个理论和计算框架来研究波浪在螺旋绳(也称为螺旋股)中的传播,螺旋绳由一根中心钢丝和两层螺旋钢丝组成。这些层通常以相反的方向缠绕,打破了连续的对称性,并引入了线和点之间的接触。本文利用非平凡曲线坐标系——双螺旋坐标系,建立了这种结构中波浪模态的存在性,定义了螺旋绳的三维重复单元格,并实现了一种特定的Bloch-Floquet波有限元方法,求解了沿双向螺旋坐标系的波传播特征问题。导线间接触面积及其对拉伸载荷的依赖关系通过赫兹接触定律下的几何互穿近似求得。通过参考测试用例的数值实验验证了该方法的有效性,包括圆柱、七线股和具有平移对称性的特殊螺旋股。最后,给出了考虑不同螺旋角和拉伸载荷的两层螺旋线的色散曲线。结果揭示了复杂的波行为,其特征是受接触面积的强烈影响的多重转向,为未来的实验和电缆无损评估的实际应用铺平了道路。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
7.00
自引率
7.30%
发文量
275
审稿时长
48 days
期刊介绍:
The European Journal of Mechanics endash; A/Solids continues to publish articles in English in all areas of Solid Mechanics from the physical and mathematical basis to materials engineering, technological applications and methods of modern computational mechanics, both pure and applied research.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


