Juxtaposing the fourth order vibrational operator perturbation theory CVPT(4) and the adaptive VCI (A-VCI): Accuracy, vibrational resonances and polyads of C2H4 and C2D4
IF 1.9
3区 物理与天体物理
Q2 OPTICS
Journal of Quantitative Spectroscopy & Radiative Transfer
Pub Date : 2025-07-29
DOI:10.1016/j.jqsrt.2025.109586
引用次数: 0
Abstract
Ab initio prediction of anharmonic vibrational spectra produces an increasing computational overhead for larger molecules, requesting a balance between an accuracy and resources. Two complementary fundamental quantum mechanical approaches, the perturbative and variational, have various strong and weak features, depending on a specific target problem. The vibrational perturbation theory (VPT) treats weak couplings and strong resonances separately, relying on somewhat artificial criteria. In contrast, the more precise but computationally intense variational configuration interaction (VCI) method treats all couplings in universal manner. The active ongoing development of approaches to solving vibrational problems requires an update of comparative benchmarks, helping to choose the best theoretical tools for a particular target. In this work, the performance of two particular modern implementations of these methods was juxtaposed: the second and fourth order operator canonical perturbation theory CVPT(2,4) and a recently proposed adaptive vibrational configuration interaction method (A-VCI). Two practically important C2H4 and C2D4 molecules and an accurate CCSD(T)/cc-pVQZ four-body sextic normal mode PES were employed for benchmarking. The comprehensive picture of vibrational resonances and the polyad quantum number was revealed in the form: . A new quadratic resonance criterion is proposed and its efficiency in elucidating polyad structures is demonstrated. A striking observation was made that CVPT(2) often produces better predictions of fundamental frequencies (e.g., RMSD for C2H4 fundamentals is 2.7 cm−1, and for C2D4 is 1.9 cm−1), while CVPT(4) demonstrates an excellent level of correlation with A-VCI results for both fundamentals and two-quanta states.
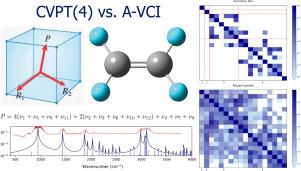
四阶振动算子摄动理论CVPT(4)与自适应VCI (A-VCI)的并置:C2H4和C2D4的精度、振动共振和多边形
对于大分子,从头算非调和振动谱的预测产生越来越多的计算开销,要求在精度和资源之间取得平衡。两个互补的基本量子力学方法,微扰和变分,有不同的强弱特征,取决于一个特定的目标问题。振动摄动理论(VPT)将弱耦合和强共振分开处理,依赖于一些人为的准则。相比之下,更精确但计算强度更大的变分组态相互作用(VCI)方法以通用方式处理所有耦合。解决振动问题的方法需要更新比较基准,这有助于为特定目标选择最佳的理论工具。在这项工作中,并置了这些方法的两种特定现代实现的性能:二阶和四阶算子正则摄动理论CVPT(2,4)和最近提出的自适应振动组态相互作用方法(a - vci)。采用两个实际重要的C2H4和C2D4分子和一个精确的CCSD(T)/cc-pVQZ四体六性正模PES进行基准测试。振动共振和多量子数的全图显示为:P[C2H4]=4(ν1+ν5+ν9+ν11)+2(ν2+ν3+ν6+ν12)+ν4+ν7+ν8+ν10。提出了一个新的二次共振判据Xj=|Vj2/(∑k(nk−mk)ωk)|,并证明了该判据在解释多晶结构中的有效性。一个引人注目的观察结果是,CVPT(2)通常对基频产生更好的预测(例如,C2H4基频的RMSD为2.7 cm−1,C2D4为1.9 cm−1),而CVPT(4)在基频和双量子态的A- vci结果中显示出极好的相关性。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
5.30
自引率
21.70%
发文量
273
审稿时长
58 days
期刊介绍:
Papers with the following subject areas are suitable for publication in the Journal of Quantitative Spectroscopy and Radiative Transfer:
- Theoretical and experimental aspects of the spectra of atoms, molecules, ions, and plasmas.
- Spectral lineshape studies including models and computational algorithms.
- Atmospheric spectroscopy.
- Theoretical and experimental aspects of light scattering.
- Application of light scattering in particle characterization and remote sensing.
- Application of light scattering in biological sciences and medicine.
- Radiative transfer in absorbing, emitting, and scattering media.
- Radiative transfer in stochastic media.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


