Using Yearly-Resolved Time Series to Disentangle Interannual Variability, Directional Change, and Pseudoturnover in Plant Community Composition
Abstract
Questions
Change in species composition over time is the result of both interannual variability, that is, year-to-year fluctuations due to weather patterns or demographic processes, and directional change, following succession or changing climatic conditions. Quantifying each component is difficult due to the confounding effects of pseudoturnover (i.e., apparent turnover due to observer error). Can yearly-resolved vegetation plot time series be used to quantify the relative contribution of these components of change, while controlling for pseudoturnover?
Location
A European beech (Fagus sylvatica) forest in Central Apennines, Italy.
Methods
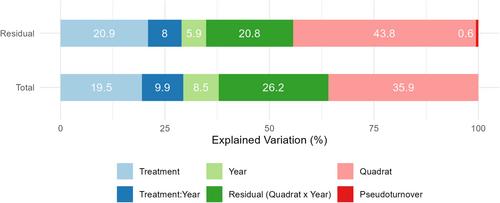
We developed an approach based on matrix decomposition and PERMANOVA to disentangle the effect of pseudoturnover, directional change, and interannual variability across nine permanent vegetation plots resurveyed for thirteen consecutive years, comparing the herb layer in a newly formed canopy gap, at the gap margins, and in the forest interior. We used helical graphs, generalized linear models, and non-metric multidimensional scaling to compare the timing and pace of vegetation change.
Results
Interannual variability and directional change accounted for similar shares of overall variation (26.7% and 28.9%, respectively). While pseudoturnover accounted for a modest 0.4%, ignoring it would result in a substantial overestimation of interannual variability. Overall, the herb layer reacted vigorously to disturbance-triggered changes in light conditions. Species richness increased from 11 to 23.3 in canopy gaps but remained stable at the gap margin and in the forest interior. The rate of change was 3.0 species/year immediately after disturbance and slowed down to 0.3 species/year after 11 years.
Conclusions
The composition of the herb layer varied substantially in the study period and showed a marked year-to-year variation even in the forest interior, where light conditions were relatively stable. A proper estimation of the interannual variability of vegetation, while crucial to benchmark the effects of disturbance in forests, should account for the confounding effect of pseudoturnover.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


