Human perception faithful curve reconstruction based on persistent homology and principal curve

Abstract

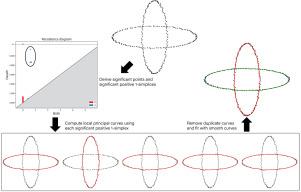
Reconstructing curves that align with human visual perception from a noisy point cloud presents a significant challenge in the field of curve reconstruction. A specific problem involves reconstructing curves from a noisy point cloud sampled from multiple intersecting curves, ensuring that the reconstructed results align with the Gestalt principles and thus produce curves faithful to human perception. This task involves identifying all potential curves from a point cloud and reconstructing approximating curves, which is critical in applications such as trajectory reconstruction, path planning, and computer vision. In this study, we propose an automatic method that utilizes the topological understanding provided by persistent homology and the local principal curve method to separate and approximate the intersecting closed curves from point clouds, ultimately achieving successful human perception faithful curve reconstruction results using B-spline curves. This technique effectively addresses noisy data clouds and intersections, as demonstrated by experimental results.