Efficient proton transport modelling for proton beam therapy and biological quantification.
IF 2.3
4区 数学
Q2 BIOLOGY
引用次数: 0
Abstract
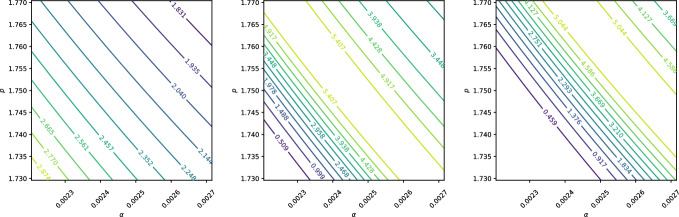
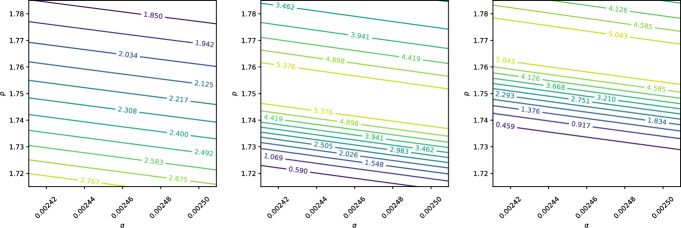
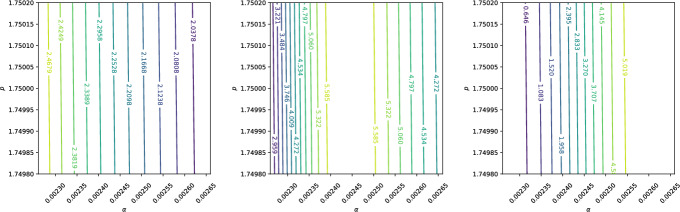
In this work, we present a fundamental mathematical model for proton transport, tailored to capture the key physical processes underpinning Proton Beam Therapy (PBT). The model provides a robust and computationally efficient framework for exploring various aspects of PBT, including dose delivery, linear energy transfer, treatment planning and the evaluation of relative biological effectiveness. Our findings highlight the potential of this model as a complementary tool to more complex and computationally intensive simulation techniques currently used in clinical practice.
质子束治疗和生物定量的有效质子输运模型。
在这项工作中,我们提出了一个质子传输的基本数学模型,旨在捕捉支撑质子束治疗(PBT)的关键物理过程。该模型为探索PBT的各个方面,包括剂量传递、线性能量转移、治疗计划和相对生物有效性评估提供了一个强大的、计算效率高的框架。我们的研究结果强调了该模型作为目前临床实践中使用的更复杂和计算密集型模拟技术的补充工具的潜力。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
3.30
自引率
5.30%
发文量
120
审稿时长
6 months
期刊介绍:
The Journal of Mathematical Biology focuses on mathematical biology - work that uses mathematical approaches to gain biological understanding or explain biological phenomena.
Areas of biology covered include, but are not restricted to, cell biology, physiology, development, neurobiology, genetics and population genetics, population biology, ecology, behavioural biology, evolution, epidemiology, immunology, molecular biology, biofluids, DNA and protein structure and function. All mathematical approaches including computational and visualization approaches are appropriate.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


