Generalized angle–orbital angular momentum Talbot effect and modulo mode sorting
IF 32.3
1区 物理与天体物理
Q1 OPTICS
引用次数: 0
Abstract
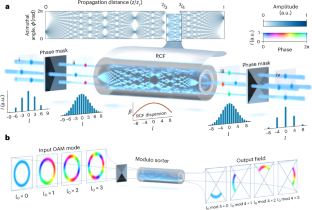
The Talbot effect describes the periodic revivals of field patterns, and is ubiquitous across wave systems. In optics, it is mostly known for its manifestations in space and time, but it is also observed in the wavevector and frequency spectra owing to the Fourier duality. Recently, the Talbot self-imaging has been shown separately in the azimuthal angle and orbital angular momentum (OAM) domains. Here we reveal the missing link between them and demonstrate the generalized angle–OAM Talbot effect. Versatile transformations of petal fields and OAM spectra are experimentally demonstrated, based on the synergy of angular Talbot phase modulation and light propagation in a ring-core fibre. Moreover, the generalized self-imaging concept leads to new realizations in mode sorting, which separate OAM modes in a modulo manner, theoretically free from any crosstalk within the congruence classes of OAM modes. We design and experimentally construct various mode sorters with excellent performance, and show the unconventional behaviour of Talbot-based sorters where neighbouring OAM modes can be mapped to positions that are far apart. Besides its fundamental interest, our work has applications in OAM-based information processing, and implies that the physical phenomena in time–frequency and angle–OAM domains are broadly connected and that their processing techniques may be borrowed interchangeably. The generalized self-imaging, or generalized Talbot, effect is demonstrated in the azimuthal angle and orbital angular momentum (OAM) domains, providing both a universal strategy for fully arbitrary control of the angular petal numbers or OAM mode spacing and a general method for the realization of efficient OAM mode sorters.

求助全文
约1分钟内获得全文
求助全文
来源期刊

Nature Photonics
物理-光学
CiteScore
54.20
自引率
1.70%
发文量
158
审稿时长
12 months
期刊介绍:
Nature Photonics is a monthly journal dedicated to the scientific study and application of light, known as Photonics. It publishes top-quality, peer-reviewed research across all areas of light generation, manipulation, and detection.
The journal encompasses research into the fundamental properties of light and its interactions with matter, as well as the latest developments in optoelectronic devices and emerging photonics applications. Topics covered include lasers, LEDs, imaging, detectors, optoelectronic devices, quantum optics, biophotonics, optical data storage, spectroscopy, fiber optics, solar energy, displays, terahertz technology, nonlinear optics, plasmonics, nanophotonics, and X-rays.
In addition to research papers and review articles summarizing scientific findings in optoelectronics, Nature Photonics also features News and Views pieces and research highlights. It uniquely includes articles on the business aspects of the industry, such as technology commercialization and market analysis, offering a comprehensive perspective on the field.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


