Photonic NP-Complete Problem Solver Enabled by Local Spatial Frequency Encoding
IF 6.5
1区 物理与天体物理
Q1 MATERIALS SCIENCE, MULTIDISCIPLINARY
引用次数: 0
Abstract
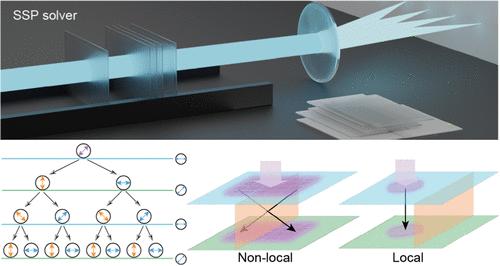
Due to the absence of known polynomial-time algorithms, NP-complete (NPC) problems, such as the subset sum problem (SSP), pose a significant challenge for electronic computers. Optical approaches, known for their inherent parallelism, low latency, and reduced power consumption, present a promising alternative. However, existing diffractive networks (DNNs) are limited to achieving only polynomial-level parallelism. In this work, we introduce an SSP solver that achieves exponential parallelism, allowing the SSP problem to be solved within polynomial time (volume). By using beam splitting in a synthetic polarization dimension to maintain a single localized optical spot and encoding spatial frequencies onto this spot, the solutions can be successfully searched in parallel. Moreover, unlike other spatial optical computing systems that require substantial thickness due to overlapping nonlocality (ONL), our system can remain remarkably thin. This thinness enables the addition of more layers without increasing the overall size, facilitating efficient 3D stacking. We have conducted a proof-of-principle experimental demonstration and discussed the advantages of our method over other state-of-the-art solutions. This work lays a strong foundation for the exploration of novel paradigms to fully utilize the parallelism of optical computing.
求助全文
约1分钟内获得全文
求助全文
来源期刊

ACS Photonics
NANOSCIENCE & NANOTECHNOLOGY-MATERIALS SCIENCE, MULTIDISCIPLINARY
CiteScore
11.90
自引率
5.70%
发文量
438
审稿时长
2.3 months
期刊介绍:
Published as soon as accepted and summarized in monthly issues, ACS Photonics will publish Research Articles, Letters, Perspectives, and Reviews, to encompass the full scope of published research in this field.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


