Dynamics and asymptotic profiles of a local-nonlocal dispersal SIR epidemic model with spatial heterogeneity

Abstract

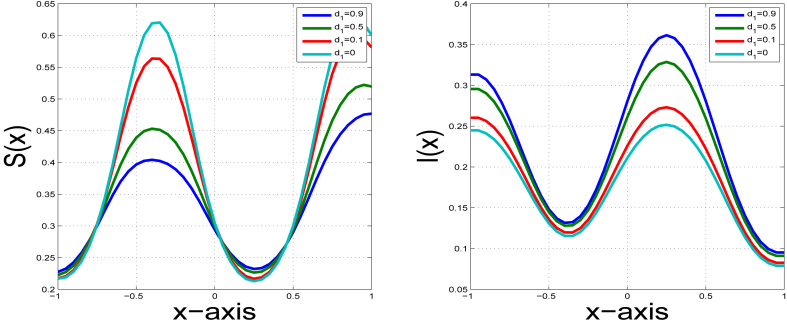
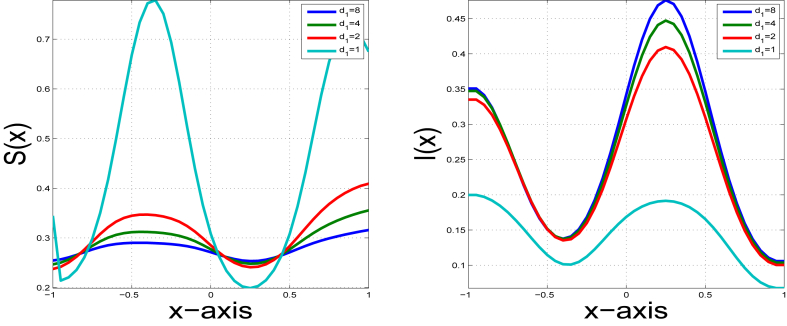
This research investigates a novel approach to modeling an SIR epidemic in a heterogeneous environment by imposing certain restrictions on population mobility. Our study reveals the influence of partially restricting the mobility of the infected population, who are allowed to diffuse locally and can be modeled using random dispersion. In contrast, the non-infective population, which includes susceptible and recovered individuals, has more freedom in their movements. This greater mobility can be modeled using nonlocal dispersion. Our approach is valid for a class of nonlocal dispersion kernels. For the analysis, we first establish the well-posedness of the solution, ensuring the existence, uniqueness, and positivity of this solution. Additionally, we identify the basic reproduction number R₀ with its threshold role. Specifically, when R₀ < 1, we prove the global asymptotic stability of the disease-free steady state. Conversely, when R₀ > 1, we demonstrate the corresponding semiflow of the model is uniformly persistent and establish behavior at endemic steady state. Lastly, we examine the asymptotic profiles of the positive steady state as the rate at which susceptible or infected individuals disperse tends to zero or infinity. Our findings reveal that when the movement of infected individuals is restricted, the infection concentrates in specific locations that may be described as the infected preferred spots.