Reply to Comment on “Synthesis and Direct Sampling of Single-Cycle Light Transients by Electron Tunneling in a Nanodevice”

Abstract

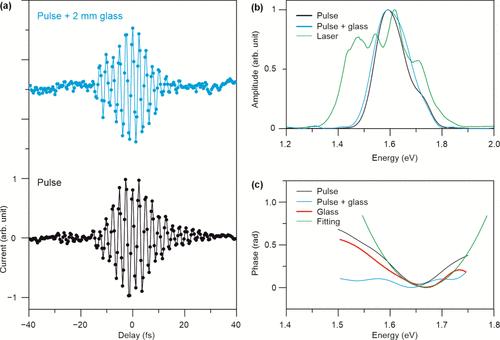
The phase in the lock-in detection, as derived in the discussions above, is (f₁ + f₀)τ – ϕ′′τ² + ϕ′′′τ³. Please note that the GDD (ϕ′′) appears with an opposite sign to both the linear phase term as well as to the second order chirp (ϕ′′′). Thus, an increase of dispersion (positive linear chirp, ϕ′′), will have an inverse effect on the temporal profiles of the laser-induced tunnelling current. The phase characterized in our experiments will also have the contribution of the dispersive phase profile of the localized surface plasmon resonance (LSPR) of the nanodevice, as also demonstrated in the following work: Nature Photonics 2021, 15, 456–460. Figure 1. Characterization of dispersion by the frequency modulation technique. (a) Comparison of the temporal profiles of the laser-induced tunnelling current measured at the lock-in frequency of f₀ when the laser pulses traverses though no glass (black curve) and ∼2 mm thick fused silica glass (blue curve). The dispersive element is placed in the path of the laser beam before it enters the interferometric setup. (b) Comparison of the spectrum of the incident laser pulses on the device (green curve) with the spectra of the laser pulses as retrieved by the Fourier-transformation of the temporal profiles shown in (a). (c) Comparison of the spectral phases of the laser pulse which traverses through the glass (blue curve) with the laser pulse which does not pass through the glass (black curve). Red curve shows the difference in the spectral phases of the two laser pulses. The sign of this spectral phase difference is flipped for a direct comparison with the theoretical estimation. The linear part of the spectral phases of the laser pulses has been removed in the analysis. Green curve shows the simulated phase profile assuming a GDD value of 50 fs². Open access funded by Max Planck Society. This article has not yet been cited by other publications.