Cautious classifier ensembles for set-valued decision-making

Abstract

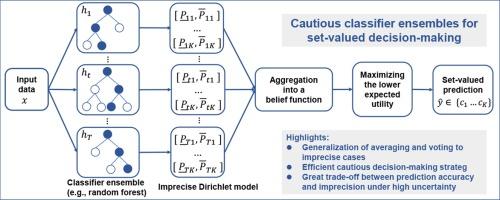
Classifiers now demonstrate impressive performances in many domains. However, in some applications where the cost of an erroneous decision is high, set-valued predictions may be preferable to classical crisp decisions, being less informative but more reliable. Cautious classifiers aim at producing such imprecise predictions so as to reduce the risk of making wrong decisions. In this paper, we describe two cautious classification approaches rooted in the ensemble learning paradigm, which consist in combining probability intervals. These intervals are aggregated within the framework of belief functions, using two proposed strategies that can be regarded as generalizations of classical averaging and voting. Our strategies aim at maximizing the lower expected discounted utility to achieve a good compromise between model accuracy and determinacy. The efficiency and performance of the proposed procedure are illustrated using imprecise decision trees, thus giving birth to cautious variants of the random forest classifier. The performance and properties of these variants are illustrated using 15 datasets.