A Complete Linkage Algorithm for Clustering Dynamic Datasets
Abstract
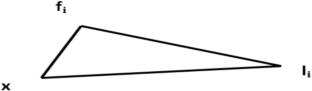
In recent years, a vital challenge faced by experts in data science is analyzing the gigantic volume of data coming at high speed. This data avalanche is not only difficult to collect but also demands high time and memory while getting processed. Clustering is a well-known solution to this problem as it not only helps in shrinking the database but also helps in gaining valuable insights from a completely unlabelled dataset. Complete Linkage Clustering is a well-known Hierarchical Clustering algorithm suitable for generating small and highly cohesive clusters but suffers from the disadvantage of high convergence time. The traditional methods require the complete dataset in advance to take a clustering decision which makes it unsuitable for clustering both large and dynamic datasets where new data points are added frequently. This is because, for every addition of data, the entire dataset will be processed again for taking a clustering decision. Our paper presents a fast Complete Linkage Clustering algorithm that uses triangle inequality to avoid a lot of redundant distance calculations making the algorithm faster and suitable for clustering both large and dynamic databases. Experiments have been conducted with various real-world datasets and Adjusted Rand Index has been used for comparing the result with the original Complete Linkage algorithm. The experimental result confirms the effectiveness of our algorithm for both static and dynamic databases.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


