Dynamic modeling and configuration transformation of origami with soft creases

Abstract

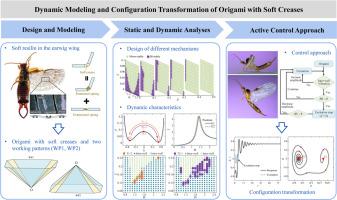
Origami has attracted much attention from scientists and engineers in recent years. Classic origami only permits rotations around creases, while origami-like structures in nature can also undergo a certain degree of extension at creases. In this paper, an earwig-inspired origami with rotational symmetry is proposed and analyzed by introducing soft creases. Such a soft crease is equivalent to a combination of a rotational spring and an extensional spring. The motion of the earwig-inspired origami is described using spherical triangles. Based on Lagrange's Equation, the nonlinear dynamic equation of the system is formulated. It is then solved by using the fourth-order Runge-Kutta method. The results of theoretical calculations are consistent with those of simulations in ADAMS. With the established framework, the bifurcation behaviors of the equilibria of the proposed system, including supercritical pitchfork and saddle-node bifurcations, are investigated. Such origami can realize both mono-stable and bi-stable mechanisms, while the corresponding design parameters are demonstrated in the design map. In particular, the properties of the bi-stable origami can vary with different equilibria. The configuration transformation could be achieved using a continuous excitation. However, it is sometimes sensitive to the initial conditions. Inspired by the working mechanism of earwig wings, a simple control approach for origami configuration transformation is proposed. The key is to stop exciting the origami when its deformation crosses an energy barrier. This work lays a foundation for the design and study of novel multi-stable and morphing structures and provides an efficient approach for their configuration transformation.