A dynamic entanglement model for adaptive networks in amorphous polymers with pH-responsive dual-shape memory effect

IF 5.4 1区化学 Q2 CHEMISTRY, MULTIDISCIPLINARY

GIANT Pub Date : 2024-11-14 DOI:10.1016/j.giant.2024.100347

Jiabin Shi , Haibao Lu , Tengfei Zheng , Yong-Qing Fu

{"title":"A dynamic entanglement model for adaptive networks in amorphous polymers with pH-responsive dual-shape memory effect","authors":"Jiabin Shi , Haibao Lu , Tengfei Zheng , Yong-Qing Fu","doi":"10.1016/j.giant.2024.100347","DOIUrl":null,"url":null,"abstract":"<div><div>The pH-responsive shape memory polymers (pH-SMPs) have recently attracted significant attention due to their unique and spontaneous actuation capabilities. However, there are few constitutive models developed to explore the working principles behind these complex shape memory behaviors. In this study, a dynamic entanglement model was developed for describing the pH-responsive shape memory effect (SME) in SMPs, in which the crosslinking points in polymer networks underwent reversible entanglements and disentanglements. Susceptible-Infected-Susceptible (SIS) model was firstly employed to formulate an entanglement probability function, which was used to identify the working principles for entanglements of polymer networks and shape recovery of the pH-SMPs. An entanglement free-energy function was further formulated to characterize the pH-responsive dual-SMEs based on the Flory-Huggins solution theory. Phase transition theory was then used to characterize glass transition behaviors and recovery strains of the pH-SMPs, by combining Gordon-Taylor and Kohlrausch-Williams-Watts (KWW) equations. Finally, the proposed model was verified using experimental results reported in the literature. This study provides a fundamental approach to explore the working principle and constitutive relationship between reversible entanglement and pH-responsive SME in SMPs.</div></div>","PeriodicalId":34151,"journal":{"name":"GIANT","volume":"21 ","pages":"Article 100347"},"PeriodicalIF":5.4000,"publicationDate":"2024-11-14","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":null,"platform":"Semanticscholar","paperid":null,"PeriodicalName":"GIANT","FirstCategoryId":"1085","ListUrlMain":"https://www.sciencedirect.com/science/article/pii/S2666542524001115","RegionNum":1,"RegionCategory":"化学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q2","JCRName":"CHEMISTRY, MULTIDISCIPLINARY","Score":null,"Total":0}

引用次数: 0

Abstract

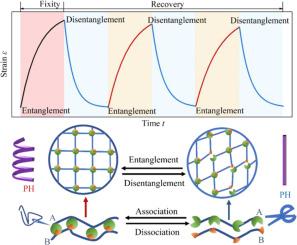
The pH-responsive shape memory polymers (pH-SMPs) have recently attracted significant attention due to their unique and spontaneous actuation capabilities. However, there are few constitutive models developed to explore the working principles behind these complex shape memory behaviors. In this study, a dynamic entanglement model was developed for describing the pH-responsive shape memory effect (SME) in SMPs, in which the crosslinking points in polymer networks underwent reversible entanglements and disentanglements. Susceptible-Infected-Susceptible (SIS) model was firstly employed to formulate an entanglement probability function, which was used to identify the working principles for entanglements of polymer networks and shape recovery of the pH-SMPs. An entanglement free-energy function was further formulated to characterize the pH-responsive dual-SMEs based on the Flory-Huggins solution theory. Phase transition theory was then used to characterize glass transition behaviors and recovery strains of the pH-SMPs, by combining Gordon-Taylor and Kohlrausch-Williams-Watts (KWW) equations. Finally, the proposed model was verified using experimental results reported in the literature. This study provides a fundamental approach to explore the working principle and constitutive relationship between reversible entanglement and pH-responsive SME in SMPs.

Abstract Image

查看原文本刊更多论文

具有 pH 响应双形记忆效应的无定形聚合物自适应网络的动态纠缠模型

pH 响应型形状记忆聚合物（pH-SMPs）因其独特的自发致动能力最近引起了广泛关注。然而，目前很少有构成模型可用于探索这些复杂形状记忆行为背后的工作原理。本研究建立了一个动态纠缠模型，用于描述 SMP 中的 pH 响应形状记忆效应（SME），其中聚合物网络中的交联点发生了可逆的纠缠和解除纠缠。首先利用易感-感染-易感（SIS）模型制定了缠结概率函数，并以此确定了聚合物网络缠结和 pH-SMP 形状复原的工作原理。在弗洛里-哈金斯溶液理论的基础上，进一步制定了纠缠自由能函数，以描述 pH 响应双 SME 的特征。然后，结合戈登-泰勒（Gordon-Taylor）方程和 Kohlrausch-Williams-Watts (KWW) 方程，使用相变理论来描述 pH-SMP 的玻璃化转变行为和恢复应变。最后，利用文献报道的实验结果对所提出的模型进行了验证。这项研究为探索 SMP 中可逆缠结和 pH 响应 SME 的工作原理和构成关系提供了一种基本方法。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

GIANT Multiple-

CiteScore

8.50

自引率

8.60%

发文量

审稿时长

42 days

期刊介绍： Giant is an interdisciplinary title focusing on fundamental and applied macromolecular science spanning all chemistry, physics, biology, and materials aspects of the field in the broadest sense. Key areas covered include macromolecular chemistry, supramolecular assembly, multiscale and multifunctional materials, organic-inorganic hybrid materials, biophysics, biomimetics and surface science. Core topics range from developments in synthesis, characterisation and assembly towards creating uniformly sized precision macromolecules with tailored properties, to the design and assembly of nanostructured materials in multiple dimensions, and further to the study of smart or living designer materials with tuneable multiscale properties.