Mallesh Baithi, Tuan Dung Nguyen, Seon Je Kim, Young-Min Kim, Dinh Loc Duong, Young Hee Lee
求助PDF
{"title":"Observation of Linear Resistance at Low Temperatures in Hole-Doped Degenerate Spin-Valley Semiconductors","authors":"Mallesh Baithi, Tuan Dung Nguyen, Seon Je Kim, Young-Min Kim, Dinh Loc Duong, Young Hee Lee","doi":"10.1021/acs.nanolett.4c04247","DOIUrl":null,"url":null,"abstract":"Linear resistivity–temperature (<i>R</i>–<i>T</i>) at low temperatures, referred to as strange metal (SM), is an unusual characteristic observed in strongly correlated systems. SM is often mingled with superconductivity and magnetism in various materials. Here, we report a linear <i>R</i>–<i>T</i> relation in a hole-doped, degenerate spin-valley (SV) semiconductor, V<sub>0.25</sub>W<sub>0.75</sub>Se<sub>2</sub>, with hole pockets in the valence band. SM emerges over a wide temperature range (1.8–150 K) without any apparent superconductivity down to 110 mK. This SM behavior is suppressed at low temperatures below 20 K in the presence of a magnetic field. The ansatz <i></i><span style=\"color: inherit;\"></span><span data-mathml='<math xmlns=\"http://www.w3.org/1998/Math/MathML\" display=\"inline\" overflow=\"scroll\"><mi>R</mi><mrow><mo stretchy=\"false\">(</mo><mi>H</mi><mo>,</mo><mi>T</mi><mo stretchy=\"false\">)</mo></mrow><mo>&#x2212;</mo><mi>R</mi><mrow><mo stretchy=\"false\">(</mo><mn>0</mn><mo>,</mo><mn>0</mn><mo stretchy=\"false\">)</mo></mrow><mo>&#x221D;</mo><msqrt><mrow><msup><mrow><mrow><mo stretchy=\"false\">(</mo><mi>&#x3B1;</mi><msub><mrow><mi>k</mi></mrow><mrow><mi mathvariant=\"normal\">B</mi></mrow></msub><mi>T</mi><mo stretchy=\"false\">)</mo></mrow></mrow><mrow><mn>2</mn></mrow></msup><mo>+</mo><msup><mrow><mrow><mo stretchy=\"false\">(</mo><mi>&#x3B3;</mi><msub><mrow><mi>&#x3BC;</mi></mrow><mrow><mi mathvariant=\"normal\">B</mi></mrow></msub><msub><mrow><mi>&#x3BC;</mi></mrow><mrow><mn>0</mn></mrow></msub><mi>H</mi><mo stretchy=\"false\">)</mo></mrow></mrow><mrow><mn>2</mn></mrow></msup></mrow></msqrt></math>' role=\"presentation\" style=\"position: relative;\" tabindex=\"0\"><nobr aria-hidden=\"true\"><span overflow=\"scroll\" style=\"width: 20.969em; display: inline-block;\"><span style=\"display: inline-block; position: relative; width: 19.037em; height: 0px; font-size: 110%;\"><span style=\"position: absolute; clip: rect(1.139em, 1019.04em, 3.298em, -999.997em); top: -2.554em; left: 0em;\"><span><span style=\"font-family: STIXMathJax_Normal-italic;\">𝑅</span><span><span style=\"font-family: STIXMathJax_Main;\">(</span><span style=\"font-family: STIXMathJax_Normal-italic;\">𝐻<span style=\"display: inline-block; overflow: hidden; height: 1px; width: 0.06em;\"></span></span><span style=\"font-family: STIXMathJax_Main;\">,</span><span style=\"font-family: STIXMathJax_Normal-italic; padding-left: 0.173em;\">𝑇<span style=\"display: inline-block; overflow: hidden; height: 1px; width: 0.116em;\"></span></span><span style=\"font-family: STIXMathJax_Main;\">)</span></span><span style=\"font-family: STIXMathJax_Main; padding-left: 0.23em;\">−</span><span style=\"font-family: STIXMathJax_Normal-italic; padding-left: 0.23em;\">𝑅</span><span><span style=\"font-family: STIXMathJax_Main;\">(</span><span style=\"font-family: STIXMathJax_Main;\">0</span><span style=\"font-family: STIXMathJax_Main;\">,</span><span style=\"font-family: STIXMathJax_Main; padding-left: 0.173em;\">0</span><span style=\"font-family: STIXMathJax_Main;\">)</span></span><span style=\"font-family: STIXMathJax_Main; padding-left: 0.344em;\">∝</span><span style=\"padding-left: 0.344em;\"><span style=\"display: inline-block; position: relative; width: 10.23em; height: 0px;\"><span style=\"position: absolute; clip: rect(2.901em, 1009.15em, 4.378em, -999.997em); top: -3.974em; left: 1.082em;\"><span><span><span><span style=\"display: inline-block; position: relative; width: 3.412em; height: 0px;\"><span style=\"position: absolute; clip: rect(3.128em, 1002.9em, 4.321em, -999.997em); top: -3.974em; left: 0em;\"><span><span><span style=\"font-family: STIXMathJax_Main;\">(</span><span style=\"font-family: STIXMathJax_Normal-italic;\">𝛼<span style=\"display: inline-block; overflow: hidden; height: 1px; width: 0.003em;\"></span></span><span><span style=\"display: inline-block; position: relative; width: 1.082em; height: 0px;\"><span style=\"position: absolute; clip: rect(3.128em, 1000.51em, 4.151em, -999.997em); top: -3.974em; left: 0em;\"><span><span style=\"font-family: STIXMathJax_Normal-italic;\">𝑘</span></span><span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"position: absolute; top: -3.804em; left: 0.571em;\"><span><span style=\"font-size: 70.7%; font-family: STIXMathJax_Main;\">B</span></span><span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span></span></span><span style=\"font-family: STIXMathJax_Normal-italic;\">𝑇<span style=\"display: inline-block; overflow: hidden; height: 1px; width: 0.116em;\"></span></span><span style=\"font-family: STIXMathJax_Main;\">)</span></span></span><span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"position: absolute; top: -4.372em; left: 2.957em;\"><span><span style=\"font-size: 70.7%; font-family: STIXMathJax_Main;\">2</span></span><span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span></span></span><span style=\"font-family: STIXMathJax_Main; padding-left: 0.23em;\">+</span><span style=\"padding-left: 0.23em;\"><span style=\"display: inline-block; position: relative; width: 4.605em; height: 0px;\"><span style=\"position: absolute; clip: rect(3.128em, 1004.15em, 4.378em, -999.997em); top: -3.974em; left: 0em;\"><span><span><span style=\"font-family: STIXMathJax_Main;\">(</span><span style=\"font-family: STIXMathJax_Normal-italic;\">𝛾<span style=\"display: inline-block; overflow: hidden; height: 1px; width: 0.06em;\"></span></span><span><span style=\"display: inline-block; position: relative; width: 1.139em; height: 0px;\"><span style=\"position: absolute; clip: rect(3.355em, 1000.57em, 4.321em, -999.997em); top: -3.974em; left: 0em;\"><span><span style=\"font-family: STIXMathJax_Normal-italic;\">𝜇</span></span><span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"position: absolute; top: -3.747em; left: 0.571em;\"><span><span style=\"font-size: 70.7%; font-family: STIXMathJax_Main;\">B</span></span><span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span></span></span><span><span style=\"display: inline-block; position: relative; width: 1.026em; height: 0px;\"><span style=\"position: absolute; clip: rect(3.355em, 1000.57em, 4.321em, -999.997em); top: -3.974em; left: 0em;\"><span><span style=\"font-family: STIXMathJax_Normal-italic;\">𝜇</span></span><span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"position: absolute; top: -3.747em; left: 0.571em;\"><span><span style=\"font-size: 70.7%; font-family: STIXMathJax_Main;\">0</span></span><span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span></span></span><span style=\"font-family: STIXMathJax_Normal-italic;\">𝐻<span style=\"display: inline-block; overflow: hidden; height: 1px; width: 0.06em;\"></span></span><span style=\"font-family: STIXMathJax_Main;\">)</span></span></span><span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"position: absolute; top: -4.372em; left: 4.207em;\"><span><span style=\"font-size: 70.7%; font-family: STIXMathJax_Main;\">2</span></span><span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span></span></span></span></span><span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"position: absolute; clip: rect(3.526em, 1009.15em, 3.923em, -999.997em); top: -4.94em; left: 1.082em;\"><span style=\"display: inline-block; position: relative; width: 9.151em; height: 0px;\"><span style=\"position: absolute; font-family: STIXMathJax_Symbols; top: -3.974em; left: 0em;\">⎯<span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"position: absolute; font-family: STIXMathJax_Symbols; top: -3.974em; left: 8.866em;\">⎯<span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"font-family: STIXMathJax_Symbols; position: absolute; top: -3.974em; left: 0.23em;\">⎯<span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"font-family: STIXMathJax_Symbols; position: absolute; top: -3.974em; left: 0.514em;\">⎯<span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"font-family: STIXMathJax_Symbols; position: absolute; top: -3.974em; left: 0.741em;\">⎯<span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"font-family: STIXMathJax_Symbols; position: absolute; top: -3.974em; left: 1.026em;\">⎯<span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"font-family: STIXMathJax_Symbols; position: absolute; top: -3.974em; left: 1.31em;\">⎯<span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"font-family: STIXMathJax_Symbols; position: absolute; top: -3.974em; left: 1.537em;\">⎯<span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"font-family: STIXMathJax_Symbols; position: absolute; top: -3.974em; left: 1.821em;\">⎯<span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"font-family: STIXMathJax_Symbols; position: absolute; top: -3.974em; left: 2.048em;\">⎯<span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"font-family: STIXMathJax_Symbols; position: absolute; top: -3.974em; left: 2.332em;\">⎯<span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"font-family: STIXMathJax_Symbols; position: absolute; top: -3.974em; left: 2.56em;\">⎯<span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"font-family: STIXMathJax_Symbols; position: absolute; top: -3.974em; left: 2.844em;\">⎯<span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"font-family: STIXMathJax_Symbols; position: absolute; top: -3.974em; left: 3.128em;\">⎯<span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"font-family: STIXMathJax_Symbols; position: absolute; top: -3.974em; left: 3.355em;\">⎯<span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"font-family: STIXMathJax_Symbols; position: absolute; top: -3.974em; left: 3.639em;\">⎯<span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"font-family: STIXMathJax_Symbols; position: absolute; top: -3.974em; left: 3.866em;\">⎯<span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"font-family: STIXMathJax_Symbols; position: absolute; top: -3.974em; left: 4.151em;\">⎯<span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"font-family: STIXMathJax_Symbols; position: absolute; top: -3.974em; left: 4.435em;\">⎯<span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"font-family: STIXMathJax_Symbols; position: absolute; top: -3.974em; left: 4.662em;\">⎯<span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"font-family: STIXMathJax_Symbols; position: absolute; top: -3.974em; left: 4.946em;\">⎯<span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"font-family: STIXMathJax_Symbols; position: absolute; top: -3.974em; left: 5.173em;\">⎯<span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"font-family: STIXMathJax_Symbols; position: absolute; top: -3.974em; left: 5.457em;\">⎯<span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"font-family: STIXMathJax_Symbols; position: absolute; top: -3.974em; left: 5.741em;\">⎯<span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"font-family: STIXMathJax_Symbols; position: absolute; top: -3.974em; left: 5.969em;\">⎯<span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"font-family: STIXMathJax_Symbols; position: absolute; top: -3.974em; left: 6.253em;\">⎯<span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"font-family: STIXMathJax_Symbols; position: absolute; top: -3.974em; left: 6.48em;\">⎯<span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"font-family: STIXMathJax_Symbols; position: absolute; top: -3.974em; left: 6.764em;\">⎯<span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"font-family: STIXMathJax_Symbols; position: absolute; top: -3.974em; left: 7.048em;\">⎯<span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"font-family: STIXMathJax_Symbols; position: absolute; top: -3.974em; left: 7.276em;\">⎯<span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"font-family: STIXMathJax_Symbols; position: absolute; top: -3.974em; left: 7.56em;\">⎯<span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"font-family: STIXMathJax_Symbols; position: absolute; top: -3.974em; left: 7.787em;\">⎯<span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"font-family: STIXMathJax_Symbols; position: absolute; top: -3.974em; left: 8.071em;\">⎯<span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"font-family: STIXMathJax_Symbols; position: absolute; top: -3.974em; left: 8.355em;\">⎯<span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"font-family: STIXMathJax_Symbols; position: absolute; top: -3.974em; left: 8.582em;\">⎯<span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span></span><span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"position: absolute; clip: rect(2.276em, 1001.08em, 4.435em, -999.997em); top: -3.69em; left: 0em;\"><span style=\"font-family: STIXMathJax_Size1;\">√</span><span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span></span></span></span><span style=\"display: inline-block; width: 0px; height: 2.56em;\"></span></span></span><span style=\"display: inline-block; overflow: hidden; vertical-align: -0.684em; border-left: 0px solid; width: 0px; height: 2.191em;\"></span></span></nobr><span role=\"presentation\"><math display=\"inline\" overflow=\"scroll\" xmlns=\"http://www.w3.org/1998/Math/MathML\"><mi>R</mi><mrow><mo stretchy=\"false\">(</mo><mi>H</mi><mo>,</mo><mi>T</mi><mo stretchy=\"false\">)</mo></mrow><mo>−</mo><mi>R</mi><mrow><mo stretchy=\"false\">(</mo><mn>0</mn><mo>,</mo><mn>0</mn><mo stretchy=\"false\">)</mo></mrow><mo>∝</mo><msqrt><mrow><msup><mrow><mrow><mo stretchy=\"false\">(</mo><mi>α</mi><msub><mrow><mi>k</mi></mrow><mrow><mi mathvariant=\"normal\">B</mi></mrow></msub><mi>T</mi><mo stretchy=\"false\">)</mo></mrow></mrow><mrow><mn>2</mn></mrow></msup><mo>+</mo><msup><mrow><mrow><mo stretchy=\"false\">(</mo><mi>γ</mi><msub><mrow><mi>μ</mi></mrow><mrow><mi mathvariant=\"normal\">B</mi></mrow></msub><msub><mrow><mi>μ</mi></mrow><mrow><mn>0</mn></mrow></msub><mi>H</mi><mo stretchy=\"false\">)</mo></mrow></mrow><mrow><mn>2</mn></mrow></msup></mrow></msqrt></math></span></span><script type=\"math/mml\"><math display=\"inline\" overflow=\"scroll\"><mi>R</mi><mrow><mo stretchy=\"false\">(</mo><mi>H</mi><mo>,</mo><mi>T</mi><mo stretchy=\"false\">)</mo></mrow><mo>−</mo><mi>R</mi><mrow><mo stretchy=\"false\">(</mo><mn>0</mn><mo>,</mo><mn>0</mn><mo stretchy=\"false\">)</mo></mrow><mo>∝</mo><msqrt><mrow><msup><mrow><mrow><mo stretchy=\"false\">(</mo><mi>α</mi><msub><mrow><mi>k</mi></mrow><mrow><mi mathvariant=\"normal\">B</mi></mrow></msub><mi>T</mi><mo stretchy=\"false\">)</mo></mrow></mrow><mrow><mn>2</mn></mrow></msup><mo>+</mo><msup><mrow><mrow><mo stretchy=\"false\">(</mo><mi>γ</mi><msub><mrow><mi>μ</mi></mrow><mrow><mi mathvariant=\"normal\">B</mi></mrow></msub><msub><mrow><mi>μ</mi></mrow><mrow><mn>0</mn></mrow></msub><mi>H</mi><mo stretchy=\"false\">)</mo></mrow></mrow><mrow><mn>2</mn></mrow></msup></mrow></msqrt></math></script> yields the γ/α ratio of ∼4, larger than the previous reports. The observed SM over a wide temperature range is explained by a spin–orbit coupling (SOC)-mediated SV pair with strong correlation effects, analogous to a phonon-mediated Cooper pair in superconductivity. This finding opens possible routes for understanding strange metal behavior through the interplay of strong SOC and strong Coulomb interactions.","PeriodicalId":53,"journal":{"name":"Nano Letters","volume":"8 1","pages":""},"PeriodicalIF":9.6000,"publicationDate":"2024-11-20","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":null,"platform":"Semanticscholar","paperid":null,"PeriodicalName":"Nano Letters","FirstCategoryId":"88","ListUrlMain":"https://doi.org/10.1021/acs.nanolett.4c04247","RegionNum":1,"RegionCategory":"材料科学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q1","JCRName":"CHEMISTRY, MULTIDISCIPLINARY","Score":null,"Total":0}
引用次数: 0
引用
批量引用
Abstract
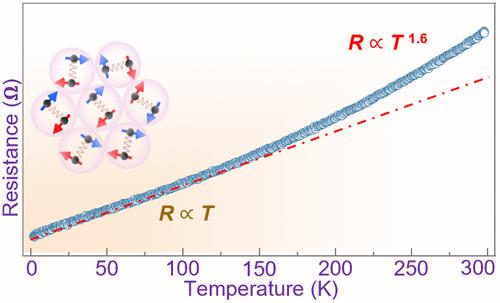
Linear resistivity–temperature (
R –
T ) at low temperatures, referred to as strange metal (SM), is an unusual characteristic observed in strongly correlated systems. SM is often mingled with superconductivity and magnetism in various materials. Here, we report a linear
R –
T relation in a hole-doped, degenerate spin-valley (SV) semiconductor, V
0.25 W
0.75 Se
2 , with hole pockets in the valence band. SM emerges over a wide temperature range (1.8–150 K) without any apparent superconductivity down to 110 mK. This SM behavior is suppressed at low temperatures below 20 K in the presence of a magnetic field. The ansatz
𝑅 ( 𝐻 , 𝑇 ) − 𝑅 ( 0 , 0 ) ∝ ( 𝛼 𝑘 B 𝑇 ) 2 + ( 𝛾 𝜇 B 𝜇 0 𝐻 ) 2 ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ ⎯ √ R ( H , T ) − R ( 0 , 0 ) ∝ ( α k B T ) 2 + ( γ μ B μ 0 H ) 2 yields the γ/α ratio of ∼4, larger than the previous reports. The observed SM over a wide temperature range is explained by a spin–orbit coupling (SOC)-mediated SV pair with strong correlation effects, analogous to a phonon-mediated Cooper pair in superconductivity. This finding opens possible routes for understanding strange metal behavior through the interplay of strong SOC and strong Coulomb interactions.
在掺杂空穴的退化自旋谷半导体中观察低温下的线性电阻
低温下的线性电阻率-温度(R-T),即奇异金属(SM),是在强相关系统中观察到的一种不寻常特性。在各种材料中,奇异金属常常与超导性和磁性混杂在一起。在这里,我们报告了一种掺杂空穴的退化自旋谷(SV)半导体 V0.25W0.75Se2(价带中有空穴)中的线性 R-T 关系。SM 出现在很宽的温度范围(1.8-150 K)内,在 110 mK 以下没有任何明显的超导现象。在磁场作用下,这种 SM 行为在低于 20 K 的低温下被抑制。公式 𝑅(𝐻,𝑇)-𝑅(0,0)∝(𝛼𝑘B𝑇)2+(𝛾𝜇B0𝐻)2⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯√R(H、T)-R(0,0)∝(αkBT)2+(γμBμ0H)2R(H,T)-R(0,0)∝(αkBT)2+(γμBμ0H)2得到的γ/α比值为∼4,大于之前的报告。在很宽的温度范围内观察到的SM是由自旋轨道耦合(SOC)介导的具有强相关效应的SV对解释的,类似于超导中声子介导的库珀对。这一发现为通过强自旋轨道耦合和强库仑相互作用的相互作用来理解奇异金属行为开辟了可能的途径。
本文章由计算机程序翻译,如有差异,请以英文原文为准。

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


