A continuum magneto-viscoelastic model for isotropic soft magnetorheological elastomers: experiments, theory and numerical implementation

Abstract

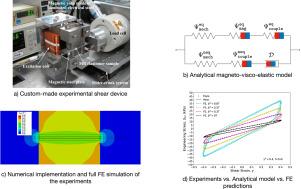
This study deals with the experimental, theoretical and numerical investigation of the nonlinear viscoelastic response of magnetically soft magnetorheological elastomers (commonly known as $s$-MREs and denoted here simply as MREs) subjected to combined magnetic and simple shear loads. We consider a fairly soft mechanically MRE. The experiments show a strong effect of the magnetic field on the resulting viscosity and hence dissipated energy expanded by the material during a simple shear cycle. Moreover, the effect of frequency on the response is weak indicating strongly nonlinear viscous effects similar to non-Newtonian fluids. An analytical magneto-viscoelastic model is proposed exhibiting magneto-mechanical coupling at both equilibrium and non-equilibrium energies as well as on the dissipation potential. The model is calibrated by solving in a semi-analytical way a simplified boundary value problem (BVP) of an infinite thin MRE strip embedded in an infinite air domain. These simplified solutions are cross-validated by full-field finite element simulations of the experimental setup showing very good agreement between the experimental data and model estimates. This illustrates the validity of the simplified material model for the proposed experimental setup and sets the ground for a more universal experimental protocol to characterize properly the finite strain response of MREs more generally.