Analysis and control of saddle-node bifurcation based on continuum model with headway fluctuation
IF 4.6
2区 物理与天体物理
Q1 PHYSICS, MULTIDISCIPLINARY
引用次数: 0
Abstract
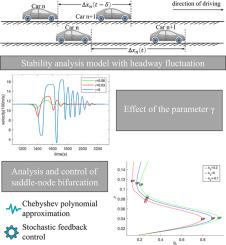
This paper presents a new traffic flow stability model suitable for bifurcation analysis based on headway fluctuation, aiming to reflect unstable characteristics such as traffic congestion to predict traffic congestion or how traffic flow stability changes under specific parameter values. Our method combines bifurcation theory and traffic flow theory to thoroughly examine congestion and stability mutation behavior near equilibrium and bifurcation points by using precise analysis tools, seeking the formation mechanism of traffic congestion and other related phenomena. Based on the stability model, the study proves the existence condition of saddle-node bifurcation and identifies the unstable bifurcation point of the traffic system. To effectively manage the unstable bifurcation point, we have developed a control scheme using Chebyshev polynomial approximation and stochastic feedback control. It enables us to shift the unstable bifurcation point and implement optimal traffic flow control and congestion prevention strategies. The bifurcation analysis method allows for the detailed analysis of the subtle dynamic behavior of a parametric dynamic system as its parameters change. This method offers potential advantages in addressing sudden changes in traffic system stability. The bifurcation control method helps manage the system's dynamic behavior, improving traffic throughput and significantly reducing accident risk. It, in turn, contributes to enhancing road safety and the overall driving experience. Our work advances the development of macroscopic traffic flow bifurcation analysis and control and can potentially have a broader impact on the entire traffic system in specific scenarios.
基于连续模型的鞍状节点分岔分析与控制
本文提出了一种基于车流波动的适用于分岔分析的新型交通流稳定性模型,旨在反映交通拥堵等不稳定特征,以预测交通拥堵或特定参数值下交通流稳定性的变化情况。我们的方法将分岔理论与交通流理论相结合,利用精确的分析工具深入研究平衡点和分岔点附近的拥堵和稳定性突变行为,寻求交通拥堵等相关现象的形成机理。基于稳定性模型,研究证明了鞍节点分岔的存在条件,并确定了交通系统的不稳定分岔点。为了有效控制不稳定分岔点,我们开发了一种采用切比雪夫多项式近似和随机反馈控制的控制方案。它使我们能够移动不稳定分岔点,并实施最优交通流控制和拥堵预防策略。分岔分析方法可以详细分析参数动态系统在参数变化时的微妙动态行为。这种方法在应对交通系统稳定性的突然变化方面具有潜在优势。分岔控制方法有助于管理系统的动态行为,提高交通吞吐量并显著降低事故风险。这反过来又有助于提高道路安全和整体驾驶体验。我们的工作推动了宏观交通流分岔分析和控制的发展,并有可能在特定场景下对整个交通系统产生更广泛的影响。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Chinese Journal of Physics
物理-物理:综合
CiteScore
8.50
自引率
10.00%
发文量
361
审稿时长
44 days
期刊介绍:
The Chinese Journal of Physics publishes important advances in various branches in physics, including statistical and biophysical physics, condensed matter physics, atomic/molecular physics, optics, particle physics and nuclear physics.
The editors welcome manuscripts on:
-General Physics: Statistical and Quantum Mechanics, etc.-
Gravitation and Astrophysics-
Elementary Particles and Fields-
Nuclear Physics-
Atomic, Molecular, and Optical Physics-
Quantum Information and Quantum Computation-
Fluid Dynamics, Nonlinear Dynamics, Chaos, and Complex Networks-
Plasma and Beam Physics-
Condensed Matter: Structure, etc.-
Condensed Matter: Electronic Properties, etc.-
Polymer, Soft Matter, Biological, and Interdisciplinary Physics.
CJP publishes regular research papers, feature articles and review papers.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


