A novel formulation for heat conduction using non-convex meshes based on smoothed finite element method
IF 5
2区 工程技术
Q1 ENGINEERING, MECHANICAL
International Journal of Heat and Mass Transfer
Pub Date : 2024-11-12
DOI:10.1016/j.ijheatmasstransfer.2024.126310
引用次数: 0
Abstract
A novel formulation for non-convex polygon mesh based on cell-based smoothed finite element method (CS-FEM) is presented for analyzing heat conduction. The major ingredient of this article include: 1) An inverse coordinate mapping method is proposed by using arbitrary polygons of shapes such as "dog", "bird", "cow" obtained from images to discretize the problem domain; 2) The Ear clipping triangulation technique is used to construct a triangular smoothing domain consisting only of field nodes; 3) The element integral is transformed into the boundary integral of triangular smoothing domain, thereby achieving temperature gradient smoothing operation, using the gradient smoothing technique, Well behaved smoothed stiffness matrix is achieved through the gradient smoothing technique of S-FEM in concave polygon elements without the need to construct additional stability terms. Based on the weakened weak form theory, the discretized system equations of heat conduction problem are established, which a symmetric and well-conditioned. The efficacy and robustness of the proposed method has been has been demonstrated through a number of benchmark examples including multi-material systems. It can effectively solve heat conduction problems using concave polygon elements, allowing materials with complex configuration being effectively modeled.
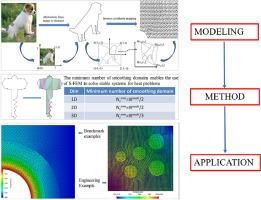
基于平滑有限元法的非凸网格热传导新公式
本文提出了一种基于单元平滑有限元法(CS-FEM)的非凸多边形网格新公式,用于分析热传导。本文的主要内容包括1) 提出了一种反坐标映射方法,使用从图像中获取的 "狗"、"鸟"、"牛 "等形状的任意多边形来离散问题域;2) 使用 "Ear clipping triangulation "技术来构建仅由场节点组成的三角形平滑域;3) 将元素积分转换为三角形平滑域的边界积分,从而实现温度梯度平滑操作,利用梯度平滑技术,通过 S-FEM 在凹多边形元素中的梯度平滑技术实现了良好的平滑刚度矩阵,而无需构建额外的稳定项。基于弱化弱形式理论,建立了对称且条件良好的热传导问题离散化系统方程。通过大量基准实例,包括多材料系统,证明了所提方法的有效性和稳健性。它能使用凹多边形元素有效地解决热传导问题,并能对具有复杂构造的材料进行有效建模。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
10.30
自引率
13.50%
发文量
1319
审稿时长
41 days
期刊介绍:
International Journal of Heat and Mass Transfer is the vehicle for the exchange of basic ideas in heat and mass transfer between research workers and engineers throughout the world. It focuses on both analytical and experimental research, with an emphasis on contributions which increase the basic understanding of transfer processes and their application to engineering problems.
Topics include:
-New methods of measuring and/or correlating transport-property data
-Energy engineering
-Environmental applications of heat and/or mass transfer

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


