The quantization of Maxwell theory in the Cauchy radiation gauge: Hodge decomposition and Hadamard states

Abstract

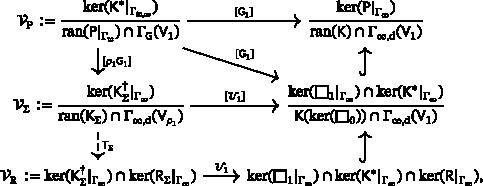
The aim of this paper is to prove the existence of Hadamard states for the Maxwell equations on any globally hyperbolic spacetime. This will be achieved by introducing a new gauge fixing condition, the Cauchy radiation gauge, that will allow to suppress all the unphysical degrees of freedom. The key ingredient for achieving this gauge is a new Hodge decomposition for differential $k$-forms in Sobolev spaces on complete (possibly noncompact) Riemannian manifolds.