Speed limits to fluctuation dynamics

Abstract

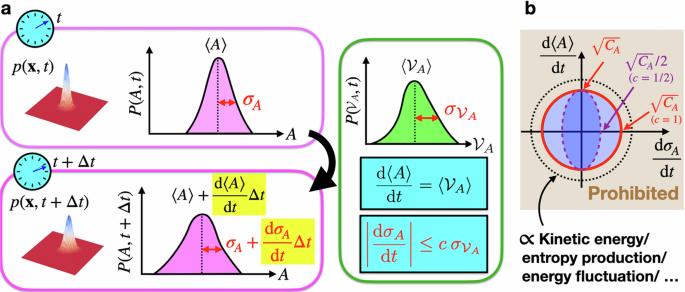
Fluctuation dynamics of an experimentally measured observable offer a primary signal for nonequilibrium systems, along with dynamics of the mean. While universal speed limits for the mean have actively been studied recently, constraints for the speed of the fluctuation have been elusive. Here, we develop a theory concerning rigorous limits to the rate of fluctuation growth. We find a principle that the speed of an observable’s fluctuation is upper bounded by the fluctuation of an appropriate observable describing velocity, which also indicates a tradeoff relation between the changes for the mean and fluctuation. We demonstrate the advantages of our inequalities for processes with non-negligible dispersion of observables, quantum work extraction, and the entanglement growth in free fermionic systems. Our results open an avenue toward a quantitative theory of fluctuation dynamics in various non-equilibrium systems encompassing quantum many-body systems and nonlinear population dynamics. Fluctuation dynamics of an observable offers a primary signal for understanding non-equilibrium statistical mechanics. Here, the author derives a principle that the speed of an observable’s fluctuation is upper bounded by the fluctuation of an observable describing velocity, which is valid for various non-equilibrium systems from quantum many-body systems to nonlinear population dynamics.