On the topology of determinantal links

IF 1 2区数学 Q1 MATHEMATICS

Journal of the London Mathematical Society-Second Series Pub Date : 2024-11-01 DOI:10.1112/jlms.70012

Matthias Zach

{"title":"On the topology of determinantal links","authors":"Matthias Zach","doi":"10.1112/jlms.70012","DOIUrl":null,"url":null,"abstract":"We study sections <math>\n <semantics>\n <mrow>\n <mo>(</mo>\n <msub>\n <mi>D</mi>\n <mi>k</mi>\n </msub>\n <mo>∩</mo>\n <msubsup>\n <mi>M</mi>\n <mrow>\n <mi>m</mi>\n <mo>,</mo>\n <mi>n</mi>\n </mrow>\n <mi>s</mi>\n </msubsup>\n <mo>,</mo>\n <mn>0</mn>\n <mo>)</mo>\n </mrow>\n <annotation>$(D_k\\cap M_{m,n}^s,0)$</annotation>\n </semantics></math> of the generic determinantal varieties <math>\n <semantics>\n <mrow>\n <msubsup>\n <mi>M</mi>\n <mrow>\n <mi>m</mi>\n <mo>,</mo>\n <mi>n</mi>\n </mrow>\n <mi>s</mi>\n </msubsup>\n <mo>=</mo>\n <mrow>\n <mo>{</mo>\n <mi>φ</mi>\n <mo>∈</mo>\n <msup>\n <mi>C</mi>\n <mrow>\n <mi>m</mi>\n <mo>×</mo>\n <mi>n</mi>\n </mrow>\n </msup>\n <mo>:</mo>\n <mo>rank</mo>\n <mi>φ</mi>\n <mo><</mo>\n <mi>s</mi>\n <mo>}</mo>\n </mrow>\n </mrow>\n <annotation>$M_{m,n}^s = \\lbrace \\varphi \\in \\mathbb {C}^{m\\times n}: \\operatorname{rank}\\varphi &lt;s \\rbrace$</annotation>\n </semantics></math> by generic hyperplanes <math>\n <semantics>\n <msub>\n <mi>D</mi>\n <mi>k</mi>\n </msub>\n <annotation>$D_k$</annotation>\n </semantics></math> of various codimensions <math>\n <semantics>\n <mi>k</mi>\n <annotation>$k$</annotation>\n </semantics></math>, the polar multiplicities of these sections, and the cohomology of their real and complex links. Such complex links were shown to provide the basic building blocks in a bouquet decomposition for the (determinantal) smoothings of smoothable isolated determinantal singularities. The detailed vanishing topology of such singularities was still not fully understood beyond isolated complete intersections and a few further special cases. Our results now allow to compute all the cohomology with integer coefficients below the middle degree and the middle Betti number for any determinantal smoothing.","PeriodicalId":49989,"journal":{"name":"Journal of the London Mathematical Society-Second Series","volume":null,"pages":null},"PeriodicalIF":1.0000,"publicationDate":"2024-11-01","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://onlinelibrary.wiley.com/doi/epdf/10.1112/jlms.70012","citationCount":"0","resultStr":null,"platform":"Semanticscholar","paperid":null,"PeriodicalName":"Journal of the London Mathematical Society-Second Series","FirstCategoryId":"100","ListUrlMain":"https://onlinelibrary.wiley.com/doi/10.1112/jlms.70012","RegionNum":2,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q1","JCRName":"MATHEMATICS","Score":null,"Total":0}

引用次数: 0

Abstract

We study sections $(D_{k} \cap M_{m, n}^{s}, 0)$ of the generic determinantal varieties $M_{m, n}^{s} = {φ \in C^{m \times n} : rank φ < s}$ by generic hyperplanes $D_{k}$ of various codimensions $k$ , the polar multiplicities of these sections, and the cohomology of their real and complex links. Such complex links were shown to provide the basic building blocks in a bouquet decomposition for the (determinantal) smoothings of smoothable isolated determinantal singularities. The detailed vanishing topology of such singularities was still not fully understood beyond isolated complete intersections and a few further special cases. Our results now allow to compute all the cohomology with integer coefficients below the middle degree and the middle Betti number for any determinantal smoothing.

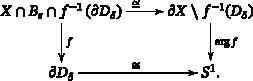
Abstract Image

查看原文本刊更多论文

论行列式链接的拓扑结构

我们研究一般行列式变量 M m , n s = { φ ∈ C m × n : rank φ < s } 的截面 ( D k ∩ M m , n s , 0 ) $(D_k\cap M_{m,n}^s,0)$ 。 $M_{m,n}^s = \lbrace \varphi \in \mathbb {C}^{m\times n}：\由不同同维度 k $k$ 的一般超平面 D k $D_k$ 、这些截面的极乘数以及它们的实链接和复链接的同调所构成的操作名{rank}\varphi <s \rbrace$ 。研究表明，这些复链接为可平滑孤立行列式奇点的（行列式）平滑化提供了花束分解的基本构件。除了孤立的完全交点和其他一些特例之外，人们对这类奇点的详细消失拓扑结构仍不完全了解。现在，我们的结果可以计算任何行列式平滑化的所有中间度和中间贝蒂数以下整数系数的同调。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Journal of the London Mathematical Society-Second Series 数学-数学

CiteScore

1.90

自引率

0.00%

发文量

186

审稿时长

6-12 weeks

期刊介绍： The Journal of the London Mathematical Society has been publishing leading research in a broad range of mathematical subject areas since 1926. The Journal welcomes papers on subjects of general interest that represent a significant advance in mathematical knowledge, as well as submissions that are deemed to stimulate new interest and research activity.