Indentation of a piezoelectric FGM-coated half-space by a conical conductive punch: Approximated analytical solution
IF 5.7
1区 工程技术
Q1 ENGINEERING, MULTIDISCIPLINARY
International Journal of Engineering Science
Pub Date : 2024-10-30
DOI:10.1016/j.ijengsci.2024.104161
引用次数: 0
Abstract
Indentation of the coated piezoelectric transversely isotropic half-space by a conical conductive punch is modeled. The coating is assumed to be functionally-graded (continuously inhomogeneous in depth) with all group of electromechanical properties varying independently in depth according to arbitrary continuous functions or piecewise homogeneous. The problem is described mathematically in terms of linear electroelasticity and reduced to solution of a system of dual integral equations using the Hankel’s integral transformations. Closed-form approximated analytical solution of this system is obtained using the bilateral asymptotic method taking into account asymptotic properties of the kernel transforms. Expressions for the contact pressure, electric induction are obtained in an analytical form suitable for engineering analysis as well as the relations for the indentation force, total electric charge, indentation depth, contact radius and electric potential. Analytical form of results clearly demonstrates the contribution of mechanical and electric loading to the total solution and influence of the coating’s thickness and its properties on contact characteristics. Numerical results for homogeneous and two types of functionally-graded coatings illustrate features of the theoretical results in a wide range of values of relative coatings thickness.
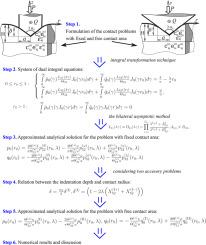
锥形导电冲头对压电 FGM 涂层半空间的压痕:近似解析解
模拟了锥形导电冲头对涂层压电横向各向同性半空间的压痕。假设涂层是功能分级的(在深度上连续不均匀),其所有机电特性组在深度上根据任意连续函数独立变化或片状均质。该问题用线性电弹性进行数学描述,并利用汉克尔积分变换简化为二元积分方程组的求解。考虑到核变换的渐近特性,利用双边渐近法获得了该系统的闭式近似解析解。以适合工程分析的解析形式获得了接触压力和电感应的表达式,以及压痕力、总电荷、压痕深度、接触半径和电动势的关系式。分析结果清楚地表明了机械负载和电负载对总解决方案的贡献,以及涂层厚度及其特性对接触特性的影响。均质涂层和两种功能分级涂层的数值结果说明了理论结果在涂层相对厚度的广泛数值范围内的特点。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

International Journal of Engineering Science
工程技术-工程:综合
CiteScore
11.80
自引率
16.70%
发文量
86
审稿时长
45 days
期刊介绍:
The International Journal of Engineering Science is not limited to a specific aspect of science and engineering but is instead devoted to a wide range of subfields in the engineering sciences. While it encourages a broad spectrum of contribution in the engineering sciences, its core interest lies in issues concerning material modeling and response. Articles of interdisciplinary nature are particularly welcome.
The primary goal of the new editors is to maintain high quality of publications. There will be a commitment to expediting the time taken for the publication of the papers. The articles that are sent for reviews will have names of the authors deleted with a view towards enhancing the objectivity and fairness of the review process.
Articles that are devoted to the purely mathematical aspects without a discussion of the physical implications of the results or the consideration of specific examples are discouraged. Articles concerning material science should not be limited merely to a description and recording of observations but should contain theoretical or quantitative discussion of the results.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


