Modeling of equivalent strain in 2D cross-sections of open die forged components using neural networks
IF 6
Q2 ENGINEERING, INDUSTRIAL
Advances in Industrial and Manufacturing Engineering
Pub Date : 2024-10-16
DOI:10.1016/j.aime.2024.100152
引用次数: 0
Abstract
Open die forging is one of the oldest manufacturing methods known to remove defects in the ingot resulting from the casting process. The improved properties of the final component are highly dependent on the strain distribution. Although sinusoidal equations and empirical formulations have been already used to estimate the strain, they have been applied only to the core of the workpiece. In this work, a novel approach is presented to model the equivalent strain distribution in 2D cross-sections, in the direction of the press, of open die forged components using neural networks. The proposed method efficiently combines a parametric sinusoidal function with a neural network to learn the complex relationships between the process parameters and the resulting local strain. The neural network is trained on a dataset of finite element (FE) simulations of rectangular geometries that cover a wide range of aspect ratios, bite ratios, and height reductions. The presented methodology with near real-time prediction capabilities shows good agreement with FE results. Moreover, the parametric function captures the characteristic pattern of the strain distribution and reveals certain physical relationships affecting the deformation of the material. These patterns are later examined by analyzing the parameters identified in the parametric sinusoidal function.
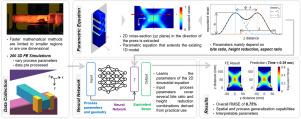
利用神经网络建立开模锻造部件二维截面等效应变模型
开模锻造是已知的最古老的制造方法之一,用于消除铸造过程中产生的钢锭缺陷。最终部件性能的改善在很大程度上取决于应变分布。虽然正弦方程和经验公式已被用于估算应变,但它们只适用于工件的核心部分。在这项工作中,提出了一种新方法,利用神经网络对开模锻造部件的二维横截面在冲压方向上的等效应变分布进行建模。所提出的方法将参数正弦函数与神经网络有效地结合起来,以学习工艺参数与所产生的局部应变之间的复杂关系。神经网络是在矩形几何形状的有限元(FE)模拟数据集上进行训练的,该数据集涵盖了宽广的长宽比、咬合比和高度缩减范围。所提出的方法具有近乎实时的预测能力,与 FE 结果显示出良好的一致性。此外,参数函数捕捉到了应变分布的特征模式,并揭示了影响材料变形的某些物理关系。随后,通过分析正弦参数函数中确定的参数,对这些模式进行了研究。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Advances in Industrial and Manufacturing Engineering
Engineering-Engineering (miscellaneous)
CiteScore
6.60
自引率
0.00%
发文量
31
审稿时长
18 days
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


