Data-driven evaluation of the Paris’ law parameters in polyethylene pipe grades — Increasing the precision of fracture mechanical lifetime estimation
IF 4.7
2区 工程技术
Q1 MECHANICS
引用次数: 0
Abstract
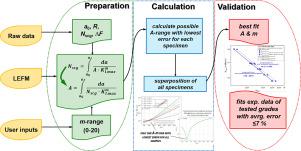
The Paris’ Law parameters and are a necessity for predicting lifetimes of structural components under static or fatigue loading that fail due to crack initiation and propagation. Conventional methods require measurements of crack growth kinetics that involve direct or indirect monitoring of physical crack extension during long-term experiments. Usually, measurement series also involve multiple specimens in order to obtain a crack growth controlled failure diagram of an investigated material under relevant load conditions. In this contribution a combination of simple numerical, statistical and analytical approaches is presented to obtain and without the need to measure actual crack growth. This is accomplished by reformulating the Paris’ Law to express as a function of . The parameter is varied within a reasonable range to generate an analytical function for that solves the equation of the Paris’ Law based lifetime for a single specimen. A subsequent superposition of all available specimens reveals an intersection of all functions at the technically relevant pair of and values that are capable of describing the lifetime of all specimens with a minimum error. The obtained best-fitting and are in good agreement with literature and are able to predict the lifetime of previously published sample data based upon cyclic Cracked Round Bar test results with an average error of 3.30 ± 2.67%.
数据驱动的聚乙烯管材牌号巴黎定律参数评估 - 提高断裂机械寿命估算的精度
帕里斯定律参数 A 和 m 是预测静态或疲劳载荷下因裂纹产生和扩展而失效的结构部件寿命的必要条件。传统方法需要测量裂纹生长动力学,包括在长期实验中直接或间接监测物理裂纹扩展。通常情况下,测量系列还涉及多个试样,以便在相关载荷条件下获得受研材料的裂纹生长受控失效图。本文将结合简单的数值、统计和分析方法,在无需测量实际裂纹生长的情况下获得 A 和 m。参数 m 在合理范围内变化可生成 A 的分析函数,该函数可求解基于巴黎定律的单个试样寿命方程。随后对所有可用试样进行叠加,就会发现所有 A 函数在 A 和 m 的技术相关值对上的交集,该值能够以最小误差描述所有试样的寿命。所获得的最佳拟合 A 和 m 与文献资料十分吻合,能够预测基于循环裂纹圆棒测试结果的先前公布的样本数据的寿命,平均误差为 3.30 ± 2.67%。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
8.70
自引率
13.00%
发文量
606
审稿时长
74 days
期刊介绍:
EFM covers a broad range of topics in fracture mechanics to be of interest and use to both researchers and practitioners. Contributions are welcome which address the fracture behavior of conventional engineering material systems as well as newly emerging material systems. Contributions on developments in the areas of mechanics and materials science strongly related to fracture mechanics are also welcome. Papers on fatigue are welcome if they treat the fatigue process using the methods of fracture mechanics.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


