Thermocapillary stability of a viscoelastic liquid film falling down above or below an inclined thick wall with slip

Abstract

Background:

Thin viscoelastic liquid films falling down walls have been investigated theoretically since many years ago due to their applications in coating and cooling of substrates. They may also be subjected to temperature gradients and have been investigated under a variety of boundary conditions. In particular, the Navier slip boundary condition has been the subject of recent research. This condition is used when at the interface between the liquid and the wall the no-slip boundary condition does not apply due to different reasons like wall small topography, chemical coatings, etc.

Methods:

The small wavenumber approximation is used to derive a nonlinear evolution equation to describe the free surface deformations of the viscoelastic liquid film falling down an inclined wall. This equation is linearized and its linear stability is investigated using normal modes. The nonlinear free surface deformations are calculated numerically by means of a normal modes expansion substituted into the nonlinear evolution equation.

Significant Findings:

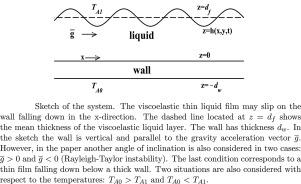
The thermocapillary stability of a thin viscoelastic film falling down a thick wall of finite thermal conductivity is investigated. Linear and nonlinear flows are examined when the interface of the liquid and the wall presents slip effects. The stability of the flow above and below (Rayleigh–Taylor) the wall is also explored. The lubrication approximation is used to derive a nonlinear evolution equation for the free surface deformation. The curves of linear growth rate, maximum growth rate and critical Marangoni number are calculated for different viscoelastic Deborah numbers. The film will be subjected to destabilizing and stabilizing Marangoni numbers. It is found that from the point of view of the linear growth rate the flow destabilizes with slip in a wavenumber range $k$ $<$ $k_{+}$. However slip stabilizes for larger wavenumbers $k$ $>$ $k_{+}$ up to the critical (cutoff) wavenumber. The results show that the Deborah number displaces $k_{+}$ to the right. When $k_{+}$ reaches the critical wavenumber by an increase of the Deborah number, slip is unable to stabilize. The corresponding critical Deborah number is derived. On the contrary, when the Deborah number is zero these slip stabilizing regions $k$ $>$ $k_{+}$ correspond to Newtonian fluids investigated in previous works. From the point of view of the maximum growth rate slip may stabilize or destabilize increasing the slip parameter depending on the magnitude of the Marangoni, Galilei and Deborah numbers. Explicit formulas were derived for the intersections where slip may change its stability properties. Numerical solutions of the free surface nonlinear evolution equation show that slip can decrease the amplitude and may stimulate the appearance of subharmonics. The effects of different wall properties are also investigated.