Coupled vibrations of thickness-extensional FBARs under stress-strain biasing state
IF 7.1
1区 工程技术
Q1 ENGINEERING, MECHANICAL
International Journal of Mechanical Sciences
Pub Date : 2024-09-21
DOI:10.1016/j.ijmecsci.2024.109748
引用次数: 0
Abstract
The method of frequency spectrum quantitative prediction (FSQP) is extended to investigate high-frequency and mode-coupling vibrations of piezoelectric film bulk acoustic resonators (FBARs) subject to initial stress-strain biasing fields for the first time. In numerical examples, we explore the cases of uniaxial compressive and tensile initial stresses along the in-plane and thickness directions, respectively. Derived from the nonlinear electroelastic theory, the governing and constitutive equations for piezoelectric films under complex stress-strain biasing states are formulated. Based on these formulations, the first step of the FSQP involves obtaining exact dispersion curves of bulk waves propagating in FBARs with different stress-strain biasing fields through the classical displacement method. Subsequently, mode-coupling solutions of physical fields are constructed for the prestressed FBARs operating with the thickness-extensional mode by superimposing relevant eigenmodes in dispersion curves. The second step of the FSQP involves deriving Hamilton's principle of piezoelectric film with initial stress-strain biasing fields using the perturbation method. Finally, the frequency spectrograms describing coupling vibration intensities between the thickness-extensional mode and unwanted eigenmodes are obtained by substituting mode-coupling solutions into Hamilton's principle, which verifies the effectiveness of the extended FSQP method for addressing dynamic problems in FBARs with biasing fields. The influences of both the amplitudes and orientations of initial stresses on the frequency spectral curves are examined. Mode-shape diagrams and displacement distributions of mutually coupled eigenmodes are presented to illustrate diverse mode-coupling behaviors in thickness-extensional FBARs under complex stress-strain biasing states. Numerical results indicate that the stress-strain biasing fields significantly affect the electromechanical properties of piezoelectric films, including effective elastic, piezoelectric, and dielectric constants. Consequently, these stress-strain biasing states exert substantial changes in frequencies and propagation wavenumbers of various mode branches within frequency ranges of the thickness-extensional mode branch. Furthermore, due to changes in propagation wavenumber, frequency spectral curves experience remarkable horizontal shifts along the length-to-thickness ratio axis, significantly altering mode-coupling behaviors of FBARs. Induced initial strains can enhance shift amplitudes of frequency spectral curves caused by initial stresses. In addition, stress-strain biasing fields result in significant shifts of frequency spectral curves along the frequency axis through the strain-stiffening or -softening effect, which can be harnessed to modulate resonance frequencies of FBARs. This study offers a solid foundation for frequency tunability, mode-coupling control, and structural designs in FBAR devices with residual stresses.
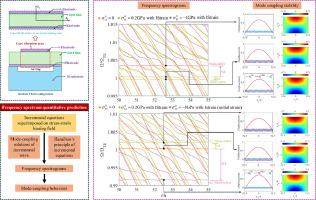
应力-应变偏置状态下厚度-拉伸 FBAR 的耦合振动
我们首次将频谱定量预测(FSQP)方法扩展用于研究压电薄膜体声谐振器(FBAR)在初始应力应变偏置场作用下的高频振动和模态耦合振动。在数值示例中,我们分别探讨了沿平面方向和厚度方向的单轴压缩和拉伸初始应力的情况。根据非线性电弹性理论,我们制定了压电薄膜在复杂应力应变偏压状态下的控制方程和构成方程。基于这些公式,FSQP 的第一步包括通过经典位移法获得在不同应力应变偏置场中传播的体波的精确频散曲线。随后,通过叠加频散曲线中的相关特征模,为以厚度-伸长模工作的预应力 FBAR 构建物理场的模耦合解。FSQP 的第二步涉及使用扰动法推导具有初始应力应变偏置场的压电薄膜的汉密尔顿原理。最后,通过将模态耦合解代入汉密尔顿原理,得到描述厚度扩展模态与不需要的特征模态之间耦合振动强度的频率谱图,从而验证了扩展 FSQP 方法在解决带偏压场的 FBAR 动态问题中的有效性。研究了初始应力的振幅和方向对频谱曲线的影响。文中给出了相互耦合特征模态的模态振型图和位移分布图,以说明在复杂的应力应变偏置状态下,厚度-伸长 FBAR 的各种模态耦合行为。数值结果表明,应力应变偏压场会显著影响压电薄膜的机电特性,包括有效弹性、压电和介电常数。因此,这些应力应变偏压态对厚度-拉伸模式分支频率范围内各种模式分支的频率和传播波数产生了重大变化。此外,由于传播波数的变化,频谱曲线会沿长度-厚度比轴发生显著的水平移动,从而极大地改变 FBAR 的模耦合行为。诱导初始应变可增强初始应力导致的频谱曲线移动幅度。此外,应力-应变偏置场还会通过应变加固或软化效应导致频谱曲线沿频率轴发生显著偏移,这可用于调节 FBAR 的共振频率。这项研究为具有残余应力的 FBAR 器件的频率可调性、模式耦合控制和结构设计奠定了坚实的基础。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

International Journal of Mechanical Sciences
工程技术-工程:机械
CiteScore
12.80
自引率
17.80%
发文量
769
审稿时长
19 days
期刊介绍:
The International Journal of Mechanical Sciences (IJMS) serves as a global platform for the publication and dissemination of original research that contributes to a deeper scientific understanding of the fundamental disciplines within mechanical, civil, and material engineering.
The primary focus of IJMS is to showcase innovative and ground-breaking work that utilizes analytical and computational modeling techniques, such as Finite Element Method (FEM), Boundary Element Method (BEM), and mesh-free methods, among others. These modeling methods are applied to diverse fields including rigid-body mechanics (e.g., dynamics, vibration, stability), structural mechanics, metal forming, advanced materials (e.g., metals, composites, cellular, smart) behavior and applications, impact mechanics, strain localization, and other nonlinear effects (e.g., large deflections, plasticity, fracture).
Additionally, IJMS covers the realms of fluid mechanics (both external and internal flows), tribology, thermodynamics, and materials processing. These subjects collectively form the core of the journal's content.
In summary, IJMS provides a prestigious platform for researchers to present their original contributions, shedding light on analytical and computational modeling methods in various areas of mechanical engineering, as well as exploring the behavior and application of advanced materials, fluid mechanics, thermodynamics, and materials processing.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


