Kitaev honeycomb antiferromagnet in a field: quantum phase diagram for general spin

Abstract

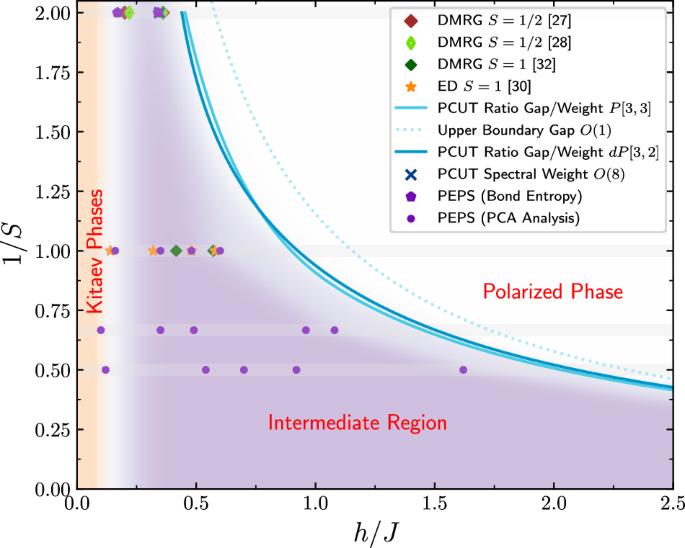
We use tensor-network methods and high-order linked-cluster expansions to explore the quantum phase diagram of the antiferromagnetic Kitaev honeycomb model in a magnetic field for general spin S values. Tensor network calculations for the pure Kitaev model confirm the absence of fluxes and spin-spin correlations beyond nearest neighbors, while revealing discrete orientational symmetry breaking for S ∈ 1, 3/2, 2, consistent with the semiclassical limit. An intermediate region between Kitaev phases and the high-field polarized phase is identified for all considered spin values, showing a sequence of potential phases characterized by distinct local magnetization patterns while the total magnetization increases smoothly as a function of the field. Linked-cluster expansions for the high-field zero-momentum gap and spectral weight indicate a quantum critical breakdown of the polarized phase, suggesting exotic physics at intermediate Kitaev couplings. The antiferromagnetic spin 1/2 Kitaev model is known to have an intermediate phase under a magnetic field before transitioning to a fully polarized state. However, the nature of this phase for higher spins remained unclear. This paper explores the quantum phase diagram of the antiferromagnetic Kitaev honeycomb model in a magnetic field using tensor-network methods and high-order linked cluster expansions, uncovering an intermediate phase with distinct local magnetization patterns across different spin values.