Correlating measures of hierarchical structures in artificial neural networks with their performance

Abstract

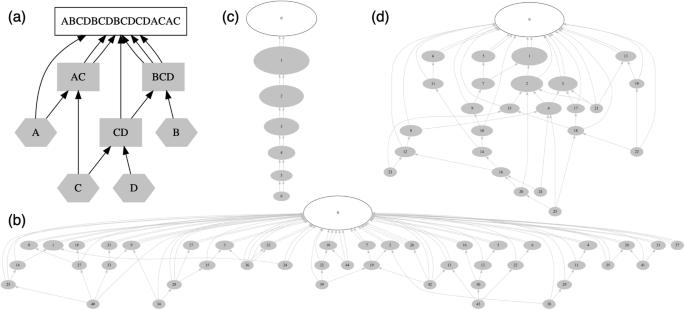
This study employs the recently developed Ladderpath approach, within the broader category of Algorithmic Information Theory (AIT), which characterizes the hierarchical and nested relationships among repeating substructures, to explore the structure-function relationship in neural networks, multilayer perceptrons (MLP), in particular. The metric order-rate η, derived from the approach, is a measure of structural orderliness: when η is in the middle range (around 0.5), the structure exhibits the richest hierarchical relationships, corresponding to the highest complexity. We hypothesize that the highest structural complexity correlates with optimal functionality. Our experiments support this hypothesis in several ways: networks with η values in the middle range show superior performance, and the training processes tend to naturally adjust η towards this range; additionally, starting neural networks with η values in this middle range appears to boost performance. Intriguingly, these findings align with observations in other distinct systems, including chemical molecules and protein sequences, hinting at a hidden regularity encapsulated by this theoretical framework.