Revised Perturbation Theory for Shifting Geometric Interfaces in High-Contrast Nanophotonics
IF 6.5
1区 物理与天体物理
Q1 MATERIALS SCIENCE, MULTIDISCIPLINARY
引用次数: 0
Abstract
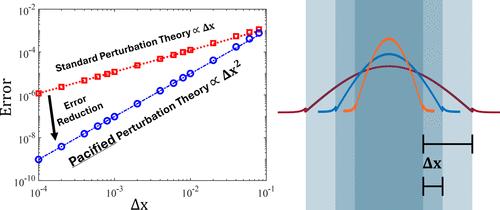
Perturbation theory is a powerful technique for solving partial differential equations, efficiently bridging the gap between analytical solutions and numerical methods. While standard perturbation theory (SPT) is commonly applied in electromagnetism to account for the effects of small changes to material properties like nonlinear susceptibilities, losses, and thermo-optic effects, i.e., so-called “bulk” perturbations, it is well-known to produce poor results when trying to account for small changes to the location of the boundaries between materials. This arises from the vectorial nature of boundary conditions in Maxwell’s equations that are enforced at the location of the original boundary and can not be “moved” via the process of linearly combining the original modes. We present an alternative formulation called pacified perturbation theory (PPT), which is able to account for this and thus make an accurate prediction of both the effective indices and the mode profiles. We demonstrate this by benchmarking our proposed PPT using the case of a high-confinement multimode nanophotonic waveguide and verify that the error associated with a first-order PPT approximation scales quadratically, unlike SPT (and its recent improvements), which fails to predict the changes in mode profiles to first order. We anticipate that our pacification procedure can be extended to higher-order corrections in perturbation theory, as well as broadened to fields beyond electromagnetism for computationally efficient predictions, where interfaces between dissimilar materials or the noncompleteness of the original mode basis (e.g., for non-Hermitian systems) thwarts standard perturbation theory.
高对比度纳米光子学中移动几何界面的修正扰动理论
扰动理论是求解偏微分方程的一种强大技术,可有效弥合分析求解与数值方法之间的差距。虽然标准扰动理论(SPT)通常应用于电磁学,以解释材料特性的微小变化所产生的影响,如非线性感性、损耗和热光效应,即所谓的 "体 "扰动,但众所周知,当试图解释材料之间边界位置的微小变化时,它产生的结果很差。这是因为麦克斯韦方程中的边界条件具有矢量性质,是在原始边界的位置上强制执行的,无法通过线性组合原始模式的过程来 "移动"。我们提出了一种称为 "平和扰动理论"(PPT)的替代方案,它能够考虑到这一点,从而准确预测有效指数和模式剖面。我们通过使用高会聚多模纳米光子波导对我们提出的 PPT 进行基准测试来证明这一点,并验证与一阶 PPT 近似值相关的误差呈二次方扩展,这与 SPT(及其最近的改进)不同,后者无法预测一阶模式剖面的变化。我们预计,我们的平息程序可以扩展到扰动理论中的高阶修正,并扩展到电磁学以外的领域,以进行计算效率高的预测,因为在这些领域中,不同材料之间的界面或原始模式基础的不完整性(例如非赫米提系统)会阻碍标准扰动理论。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

ACS Photonics
NANOSCIENCE & NANOTECHNOLOGY-MATERIALS SCIENCE, MULTIDISCIPLINARY
CiteScore
11.90
自引率
5.70%
发文量
438
审稿时长
2.3 months
期刊介绍:
Published as soon as accepted and summarized in monthly issues, ACS Photonics will publish Research Articles, Letters, Perspectives, and Reviews, to encompass the full scope of published research in this field.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


