Impact of local navigation rules on biased random walks in multiplex Markov chains

Abstract

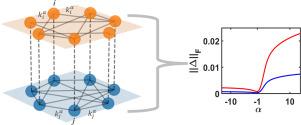
Our investigation centres on assessing the importance of a biased parameter ($\alpha$) in a multiplex Markov chain (MMC) model that is characterized by biased random walks in multiplex networks. We explore how varying complex network topologies affect the total multiplex imbalance as a function of biased parameter. Our primary finding is that the system demonstrates a gradual increase in total imbalance within both positive and negative regions of the biased parameter, with a consistent minimum value occurring at $\alpha =-1$. In contrast to the negative region, the total imbalance is consistently high when $\alpha$ is significantly positive. We perform a detailed examination of four different network structures and establish three sets of multiplex networks. In each of these networks, the second layer consists of a Regular Random network, while the first layer is either a Barabási–Albert, Erdős-Rényi, or Watts Strogatz network, depending on the set. Our results demonstrate that the combination of Barabási–Albert and Random Regular Network exhibits the highest level of right saturation imbalance. Additionally, for left saturation imbalance, the Erdős–Rényi and Random Regular combination achieve a slightly higher value. We also observe that the total amount of imbalance at $\alpha =-1$ follows a decreasing trend as the size of the network of each layer increases. Furthermore, we are also able to illustrate that the second most significant eigenvalue of the supra-transition matrix exhibits a similar pattern in response to changes in the bias parameter, aligning with the overall system’s imbalance.