On tame ramification and centers of F $F$ -purity

IF 1 2区数学 Q1 MATHEMATICS

Journal of the London Mathematical Society-Second Series Pub Date : 2024-09-26 DOI:10.1112/jlms.12993

Javier Carvajal-Rojas, Anne Fayolle

{"title":"On tame ramification and centers of \n \n F\n $F$\n -purity","authors":"Javier Carvajal-Rojas, Anne Fayolle","doi":"10.1112/jlms.12993","DOIUrl":null,"url":null,"abstract":"We introduce a notion of tame ramification for general finite covers. When specialized to the separable case, it extends to higher dimensions the classical notion of tame ramification for Dedekind domains and curves and sits nicely in between other notions of tame ramification in arithmetic geometry. However, when applied to the Frobenius map, it naturally yields the notion of center of <math>\n <semantics>\n <mi>F</mi>\n <annotation>$F$</annotation>\n </semantics></math>-purity (aka compatibly <math>\n <semantics>\n <mi>F</mi>\n <annotation>$F$</annotation>\n </semantics></math>-split subvariety). As an application, we describe the behavior of centers of <math>\n <semantics>\n <mi>F</mi>\n <annotation>$F$</annotation>\n </semantics></math>-purity under finite covers — it all comes down to a transitivity property for tame ramification in towers.","PeriodicalId":49989,"journal":{"name":"Journal of the London Mathematical Society-Second Series","volume":null,"pages":null},"PeriodicalIF":1.0000,"publicationDate":"2024-09-26","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://onlinelibrary.wiley.com/doi/epdf/10.1112/jlms.12993","citationCount":"0","resultStr":null,"platform":"Semanticscholar","paperid":null,"PeriodicalName":"Journal of the London Mathematical Society-Second Series","FirstCategoryId":"100","ListUrlMain":"https://onlinelibrary.wiley.com/doi/10.1112/jlms.12993","RegionNum":2,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q1","JCRName":"MATHEMATICS","Score":null,"Total":0}

引用次数: 0

Abstract

We introduce a notion of tame ramification for general finite covers. When specialized to the separable case, it extends to higher dimensions the classical notion of tame ramification for Dedekind domains and curves and sits nicely in between other notions of tame ramification in arithmetic geometry. However, when applied to the Frobenius map, it naturally yields the notion of center of $F$ -purity (aka compatibly $F$ -split subvariety). As an application, we describe the behavior of centers of $F$ -purity under finite covers — it all comes down to a transitivity property for tame ramification in towers.

查看原文本刊更多论文

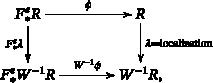
论 F $F$ 纯度的驯服斜面和中心

我们引入了一般有限盖的驯服斜伸概念。当它专门用于可分离的情况时，它将戴德金域和曲线的经典驯化斜率概念扩展到了更高维度，并很好地介于算术几何中的其他驯化斜率概念之间。然而，当应用于弗罗贝尼斯映射时，它自然会产生 F $F$ 纯度中心的概念（又称兼容 F $F$ 分裂子域）。作为一种应用，我们描述了 F $F$ -纯度中心在有限覆盖下的行为--这一切都归结为塔中驯服斜切的反证性质。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Journal of the London Mathematical Society-Second Series 数学-数学

CiteScore

1.90

自引率

0.00%

发文量

186

审稿时长

6-12 weeks

期刊介绍： The Journal of the London Mathematical Society has been publishing leading research in a broad range of mathematical subject areas since 1926. The Journal welcomes papers on subjects of general interest that represent a significant advance in mathematical knowledge, as well as submissions that are deemed to stimulate new interest and research activity.