Ideal Collision Rate of Symmetric Hexapods in a Simple Shear Flow
IF 4.3
3区 材料科学
Q1 ENGINEERING, ELECTRICAL & ELECTRONIC
引用次数: 0
Abstract
An ideal collision rate (ICR) is defined as the average rate of contact between two particles that translate and rotate with the imposed fluid flow in the absence of interparticle interactions. ICR in a simple shear flow provides an estimate of the collision rate in a flowing dilute particle suspension, and its value is known only for traditional convex shapes such as spheres and cylinders. In this work, we compute the ICR for a family of symmetric hexapods (shown in Figure 1) that are particles composed of three orthogonal cylinders with coinciding centers (forming six arms) with at least two cylinders having the same length. We employed the finite-element method to obtain the rotational dynamics of hexapods and Monte Carlo simulations to calculate their ICR. Our results indicate that the ICR for hexapods is not directly proportional to the volume of the particle, in contrast to what is observed for convex shapes such as spheres and cylinders. For hexapods of the same size, the ICR could be similar for particles with order-of-magnitude differences in their volumes and it could also vary by an order of magnitude for particles with similar volumes. Specifically for hexapods termed branched fibers, which have one longer cylinder, the ICR changes by an order of magnitude even when the shorter cylinders are significantly smaller than the longer cylinder. This change is attributed to the increase in the tumbling frequency of the particle due to hydrodynamic forces acting on the shorter arms, in addition to the increased probability of collision afforded by them. Using asymptotic theory for high-aspect ratio cylinders, we showed that the tumbling period of hexapods was proportional to an algebraic power of the ratio of its arm lengths and has a weaker logarithm relationship with the aspect ratio of its arms. The collision cross-section provided the relative cross-streamline particle separations for the most likely binary collisions in the suspensions, and its value was sensitive to the arm lengths, as well. The collision rate of hexapods also could not be estimated within an order of magnitude from existing geometric models, such as the ICR of a circumscribing convex shape, ICR for one of the individual cylinders of the hexapod, or using the particle volume times the shear rate. Our work indicates that collision rate for non-convex particles in shear flows critically depends on the shape of the particle due to nontrivial changes in the particle’s orientational dynamics, and the ICR calculation serves as a more reliable method for estimating their true collision rates in the suspension.
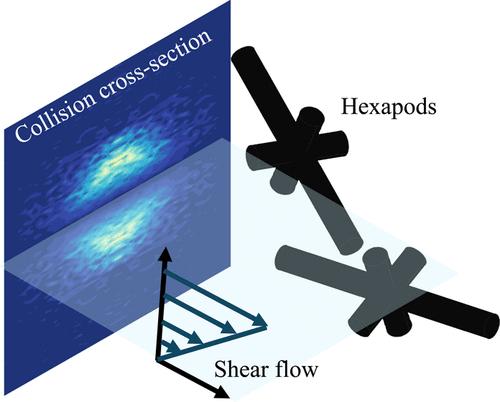
简单剪切流中对称六足动物的理想碰撞率
理想碰撞率(ICR)的定义是,在没有颗粒间相互作用的情况下,随外加流体流动而平移和旋转的两个颗粒之间的平均接触率。简单剪切流中的理想碰撞率可以估算出流动的稀颗粒悬浮液中的碰撞率,其值仅适用于传统的凸形颗粒,如球体和圆柱体。在这项工作中,我们计算了对称六面体系列(如图 1 所示)的 ICR,这些六面体是由中心重合的三个正交圆柱体(形成六个臂)组成的颗粒,其中至少有两个圆柱体具有相同的长度。我们采用有限元法获得了六角体的旋转动力学,并通过蒙特卡罗模拟计算了它们的 ICR。我们的结果表明,与球体和圆柱体等凸形颗粒不同,六足颗粒的 ICR 与颗粒的体积并不成正比。对于相同大小的六足虫来说,体积相差数量级的颗粒的 ICR 可能相似,而体积相近的颗粒的 ICR 也可能相差一个数量级。具体来说,对于有一个较长圆柱体的被称为分枝纤维的六形体,即使较短的圆柱体明显小于较长的圆柱体,ICR 也会发生一个数量级的变化。这种变化归因于作用在短臂上的流体动力增加了粒子的翻滚频率,以及短臂增加了碰撞概率。利用高长宽比圆柱体的渐近理论,我们发现六足虫的翻滚周期与其臂长之比的代数幂成正比,与其臂的长宽比的对数关系较弱。碰撞截面提供了悬浮液中最有可能发生的二元碰撞的相对交叉流线粒子间距,其值对臂长也很敏感。六足虫的碰撞率也无法从现有的几何模型中估算出一个数量级,例如圆周凸形的 ICR、六足虫单个圆柱体的 ICR 或使用粒子体积乘以剪切率。我们的研究表明,非凸颗粒在剪切流中的碰撞率主要取决于颗粒的形状,这是因为颗粒的方向动力学发生了非微不足道的变化,而 ICR 计算是估算其在悬浮液中真实碰撞率的更可靠方法。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


