A hybrid model for accurate prediction of composite longitudinal elastic modulus

Abstract

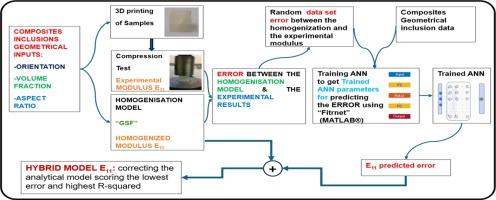
This research presents a novel hybrid model that integrates a physical-based empirical model with an Artificial Neural Network (ANN) to accurately predict the longitudinal modulus of elasticity for composites under compression. The study focuses on a composite material with a pore inclusion within an ABS plastic matrix, exploring various pore volumes, orientations, and shapes. As part of the proposed hybrid model, a regression-type neural network was trained in MATLAB® to predict and correct discrepancies between the Generalized Stiffness Formulation (GSF) homogenization-based modeling method and the collected compression experimental test results. Using MATLAB® neural network, random error datasets were used to train the feed-forward neural network, and the remaining error datasets were used for validating the performance of the proposed hybrid modeling scheme.

The hybrid model demonstrated superior performance, achieving the lowest Mean Error (ME) of 0.1684864, Mean Absolute Error (MAE) of 1.051846, Mean Squared Error (MSE) of 3.500952, and highest R-squared of 0.998797. The proposed hybrid model outperformed both the Generalized Stiffness Formulation (GSF) and standalone ANN models. The significant improvement in prediction accuracy underscores the novelty and robustness of the hybrid approach in composite material modeling. Furthermore, this method can be used to refine any existing physical model by focusing on improving these established models to match experimental results and reducing the discrepancies, which offers a more efficient and attractive strategy for accurate predictions.