Parametric instability analysis of rotors under anisotropic boundary conditions
IF 7.1
1区 工程技术
Q1 ENGINEERING, MECHANICAL
International Journal of Mechanical Sciences
Pub Date : 2024-09-16
DOI:10.1016/j.ijmecsci.2024.109739
引用次数: 0
Abstract
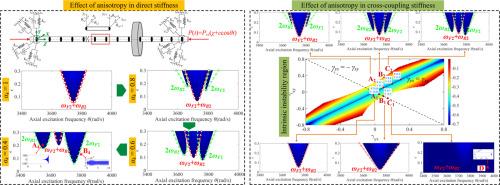
Ensuring rotor stability is a major concern in engineering, as instabilities can lead to catastrophic failures. Existing literature shows that anisotropic boundary conditions significantly affect the parametric instability characteristics of rotors under periodical axial loads. However, there is little literature systematically analyzing the formation mechanism of parametric resonance under these boundary conditions or providing a detailed classification of the parametric instability regions. Therefore, this paper presents a comprehensive parametric instability analysis of a rotor subjected to periodic axial loads under anisotropic boundary conditions. A novel approach based on the multiple scales method is proposed to address anisotropy in the boundary conditions. Using this approach, the analytical boundaries of the parametric instability regions are derived, and a proof regarding the absence of certain parametric resonances is presented. These analytical solutions are validated by numerical results obtained from the discrete transition matrix method, which form the basis for systematically investigating the effects of anisotropy in direct or cross-coupling stiffness/damping coefficients on the rotor instability. The key scientific contributions of this work include: Deriving analytical instability boundaries, providing a more efficient alternative to purely numerical methods while maintaining high accuracy; Demonstrating the absence of parametric resonance of difference type under both isotropic or anisotropic boundary conditions; Discovering that anisotropy in stiffness coefficients can induce self-interaction within a given forward or backward whirl mode, as well as interaction between two forward or two backward whirl modes, leading to additional instability regions; Reducing anisotropy in direct damping coefficients may increase critical dynamic load coefficients, potentially enhancing rotor safety; If the cross-coupling stiffness coefficients exceed the threshold for triggering intrinsic instability, the rotor may become unstable in all operating conditions. All these findings offer insights into the stability management of rotors under various operating conditions and provide valuable guidance for designing and operating safer, more efficient rotor systems.
各向异性边界条件下转子的参数失稳分析
确保转子的稳定性是工程领域的一个主要问题,因为不稳定性可能导致灾难性故障。现有文献表明,各向异性边界条件会显著影响转子在周期性轴向载荷作用下的参数失稳特性。然而,很少有文献系统地分析这些边界条件下参数共振的形成机理,或对参数失稳区域进行详细的分类。因此,本文对各向异性边界条件下承受周期性轴向载荷的转子进行了全面的参数失稳分析。本文提出了一种基于多尺度法的新方法来解决边界条件中的各向异性问题。利用这种方法,得出了参数不稳定性区域的分析边界,并证明不存在某些参数共振。离散过渡矩阵法获得的数值结果验证了这些分析解,为系统研究直接或交叉耦合刚度/阻尼系数各向异性对转子不稳定性的影响奠定了基础。这项工作的主要科学贡献包括推导出分析不稳定性边界,在保持高精度的同时,为纯数值方法提供了更有效的替代方法;证明在各向同性或各向异性边界条件下均不存在差分类型的参数共振;发现刚度系数的各向异性可在给定的前向或后向旋流模式内引起自相互作用,以及两个前向或两个后向旋流模式之间的相互作用,从而导致额外的不稳定区域;降低直接阻尼系数的各向异性可能会增加临界动载荷系数,从而提高转子的安全性;如果交叉耦合刚度系数超过了引发内在不稳定性的阈值,转子可能会在所有运行条件下变得不稳定。所有这些发现为转子在各种运行条件下的稳定性管理提供了启示,并为设计和运行更安全、更高效的转子系统提供了宝贵的指导。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

International Journal of Mechanical Sciences
工程技术-工程:机械
CiteScore
12.80
自引率
17.80%
发文量
769
审稿时长
19 days
期刊介绍:
The International Journal of Mechanical Sciences (IJMS) serves as a global platform for the publication and dissemination of original research that contributes to a deeper scientific understanding of the fundamental disciplines within mechanical, civil, and material engineering.
The primary focus of IJMS is to showcase innovative and ground-breaking work that utilizes analytical and computational modeling techniques, such as Finite Element Method (FEM), Boundary Element Method (BEM), and mesh-free methods, among others. These modeling methods are applied to diverse fields including rigid-body mechanics (e.g., dynamics, vibration, stability), structural mechanics, metal forming, advanced materials (e.g., metals, composites, cellular, smart) behavior and applications, impact mechanics, strain localization, and other nonlinear effects (e.g., large deflections, plasticity, fracture).
Additionally, IJMS covers the realms of fluid mechanics (both external and internal flows), tribology, thermodynamics, and materials processing. These subjects collectively form the core of the journal's content.
In summary, IJMS provides a prestigious platform for researchers to present their original contributions, shedding light on analytical and computational modeling methods in various areas of mechanical engineering, as well as exploring the behavior and application of advanced materials, fluid mechanics, thermodynamics, and materials processing.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


