Surfaces with Central Configuration and Dulac’s Problem for a Three Dimensional Isolated Hopf Singularity
IF 1.3
4区 数学
Q1 MATHEMATICS
引用次数: 0
Abstract
Let \(\xi \) be a real analytic vector field with an elementary isolated singularity at \(0\in \mathbb {R}^3\) and eigenvalues \(\pm bi,c\) with \(b,c\in \mathbb {R}\) and \(b\ne 0\). We prove that all cycles of \(\xi \) in a sufficiently small neighborhood of 0, if they exist, are contained in the union of finitely many subanalytic invariant surfaces, each one entirely composed of a continuum of cycles. In particular, we solve Dulac’s problem for such vector fields, i.e., finiteness of limit cycles.
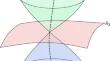
具有中心配置的曲面和三维孤立霍普夫奇点的杜拉克问题
让\(\xi \)是一个实解析向量场,在\(0\in \mathbb {R}^3\)处有一个基本孤立奇点,特征值为\(\pm bi,c\),\(b,c\in \mathbb {R}\)和\(b\ne 0\)。我们证明,在0的足够小的邻域内的(xi \)的所有循环(如果存在的话)都包含在有限多个次解析不变曲面的联合中,每个曲面都完全由循环的连续体组成。我们特别解决了这类向量场的杜拉克问题,即极限循环的有限性问题。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
3.30
自引率
7.70%
发文量
116
审稿时长
>12 weeks
期刊介绍:
Journal of Dynamics and Differential Equations serves as an international forum for the publication of high-quality, peer-reviewed original papers in the field of mathematics, biology, engineering, physics, and other areas of science. The dynamical issues treated in the journal cover all the classical topics, including attractors, bifurcation theory, connection theory, dichotomies, stability theory and transversality, as well as topics in new and emerging areas of the field.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


