Edge Zeros and Boundary Spinons in Topological Mott Insulators

Abstract

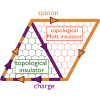
We use a real-space slave-rotor theory of the physics of topological Mott insulators, using the Kane-Mele-Hubbard model as an example, and show that a topological gap in the Green function zeros corresponds to a gap in the bulk spinon spectrum and implies a gapless band of edge zeros and a spinon edge mode. We then consider an interface between a topological Mott insulator and a conventional topological insulator showing how the spinon edge mode of the topological Mott insulator combines with the spin part of the conventional electron topological edge state, leaving a non-Fermi liquid edge mode described by a gapless propagating holon and gapped spinon state. Our work demonstrates the physical meaning of Green function zeros and shows that interfaces between conventional and Mott topological insulators are a rich source of new physics.