Estimating correlations and entanglement in the two-dimensional Heisenberg model in the strong-rung-coupling limit
IF 2.9
2区 物理与天体物理
Q2 Physics and Astronomy
引用次数: 0
Abstract
We consider the isotropic Heisenberg model in a magnetic field in the strong-rung-coupling limit on a two-dimensional (2D) rectangular zig-zag lattice of arbitrary size, and determine the one-dimensional (1D) effective model representing the low-energy manifold of the 2D model up to second order in perturbation theory. We consider a number of Hermitian operators defined on the Hilbert space of the 2D model, and systematically work out their action on the low-energy manifold, which are operators on the Hilbert space of the 1D effective model. For a class of operators among them, we demonstrate that the expectation values computed in the low-energy manifold of the 2D model can be mimicked by the expectation values of the corresponding operators in the 1D effective model even beyond the perturbation regime of the system parameters. We further argue that quantitatively estimating partial trace-based measures of entanglement in the 2D model may be done in the same fashion only in the perturbation regime. Our results and approach are expected to be useful in investigating observables and entanglement in the 2D models with large system sizes due to the advantage of using the effective 1D model with a smaller Hilbert space as a proxy.
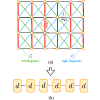
估算强环耦合极限下二维海森堡模型中的相关性和纠缠性
我们在任意大小的二维(2D)矩形之字形晶格上考虑磁场中强环耦合极限的各向同性海森堡模型,并确定代表二维模型低能流形的一维(1D)有效模型,其扰动理论达到二阶。我们考虑了定义在二维模型的希尔伯特空间上的一些赫米特算子,并系统地计算了它们在低能流形上的作用,它们是一维有效模型的希尔伯特空间上的算子。对于其中的一类算子,我们证明了在二维模型的低能流形中计算出的期望值可以通过一维有效模型中相应算子的期望值来模拟,甚至超越了系统参数的扰动机制。我们进一步论证,在二维模型中定量估计基于部分迹线的纠缠度量,也可以只在扰动机制中以同样的方式进行。由于使用具有较小希尔伯特空间的有效一维模型作为代理的优势,我们的结果和方法有望在研究具有较大系统规模的二维模型中的观测值和纠缠时发挥作用。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Physical Review A
物理-光学
CiteScore
5.40
自引率
24.10%
发文量
0
审稿时长
2.2 months
期刊介绍:
Physical Review A (PRA) publishes important developments in the rapidly evolving areas of atomic, molecular, and optical (AMO) physics, quantum information, and related fundamental concepts.
PRA covers atomic, molecular, and optical physics, foundations of quantum mechanics, and quantum information, including:
-Fundamental concepts
-Quantum information
-Atomic and molecular structure and dynamics; high-precision measurement
-Atomic and molecular collisions and interactions
-Atomic and molecular processes in external fields, including interactions with strong fields and short pulses
-Matter waves and collective properties of cold atoms and molecules
-Quantum optics, physics of lasers, nonlinear optics, and classical optics
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


