Efficiency bounds for bipartite information-thermodynamic systems
IF 2.4
3区 物理与天体物理
Q1 Mathematics
引用次数: 0
Abstract
In this paper, we introduce an approach to derive a lower bound for the entropy production rate of a subsystem by utilizing the Cauchy-Schwarz inequality. It extends to establishing comprehensive upper and lower bounds for the efficiency of two subsystems. These bounds are applicable to a wide range of Markovian stochastic processes, which enhances the accuracy in depicting the range of energy conversion efficiency between subsystems. Empirical validation is conducted using a two-quantum-dot system model, which serves to confirm the effectiveness of our inequality in refining the boundaries of efficiency.
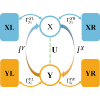
二方信息热动力系统的效率边界
本文介绍了一种利用考希-施瓦茨不等式推导子系统熵产生率下限的方法。它扩展到为两个子系统的效率建立全面的上界和下界。这些界限适用于多种马尔可夫随机过程,从而提高了描述子系统间能量转换效率范围的准确性。我们使用双量子点系统模型进行了经验验证,证实了我们的不等式在完善效率边界方面的有效性。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Physical review. E
物理-物理:流体与等离子体
CiteScore
4.60
自引率
16.70%
发文量
0
审稿时长
3.3 months
期刊介绍:
Physical Review E (PRE), broad and interdisciplinary in scope, focuses on collective phenomena of many-body systems, with statistical physics and nonlinear dynamics as the central themes of the journal. Physical Review E publishes recent developments in biological and soft matter physics including granular materials, colloids, complex fluids, liquid crystals, and polymers. The journal covers fluid dynamics and plasma physics and includes sections on computational and interdisciplinary physics, for example, complex networks.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


