Renormalization of networks with weak geometric coupling

Abstract

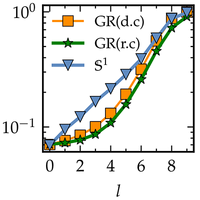
The renormalization group is crucial for understanding systems across scales, including complex networks. Renormalizing networks via network geometry, a framework in which their topology is based on the location of nodes in a hidden metric space, is one of the foundational approaches. However, the current methods assume that the geometric coupling is strong, neglecting weak coupling in many real networks. This paper extends renormalization to weak geometric coupling, showing that geometric information is essential to preserve self-similarity. Our results underline the importance of geometric effects on network topology even when the coupling to the underlying space is weak.