Bifurcation for indefinite-weighted p $p$ -Laplacian problems with slightly subcritical nonlinearity

Abstract

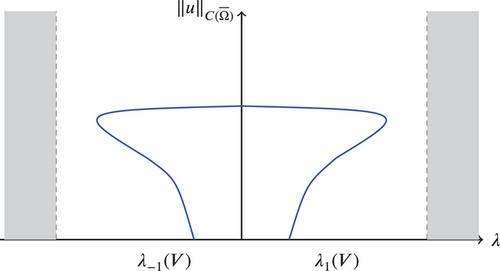
We study a superlinear elliptic boundary value problem involving the $p$-Laplacian operator, with changing sign weights. The problem has positive solutions bifurcating from the trivial solution set at the two principal eigenvalues of the corresponding linear weighted boundary value problem.

Drabek's bifurcation result applies when the nonlinearity is of power growth. We extend Drabek's bifurcation result to slightly subcritical nonlinearities. Compactness in this setting is a delicate issue obtained via Orlicz spaces.