The class group of a minimal model of a quotient singularity
IF 0.8
3区 数学
Q2 MATHEMATICS
引用次数: 0
Abstract
Let be a finite-dimensional vector space over the complex numbers and let be a finite group. We describe the class group of a minimal model (i.e., -factorial terminalization) of the linear quotient . We prove that such a class group is completely controlled by the junior elements contained in .
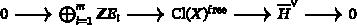
商奇点最小模型的类群
让 V $V$ 是复数上的有限维向量空间,让 G ⩽ SL ( V ) $G\leqslant \operatorname{SL}(V)$ 是有限群。我们将描述线性商 V / G $V/G$ 的最小模型(即 Q $\mathbb {Q}$ -因子终结)的类群。我们证明这样的类群完全由 G $G$ 中包含的初等元素控制。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
1.90
自引率
0.00%
发文量
198
审稿时长
4-8 weeks
期刊介绍:
Published by Oxford University Press prior to January 2017: http://blms.oxfordjournals.org/

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


