Configuration spaces as commutative monoids
IF 0.8
3区 数学
Q2 MATHEMATICS
引用次数: 0
Abstract
After one-point compactification, the collection of all unordered configuration spaces of a manifold admits a commutative multiplication by superposition of configurations. We explain a simple (derived) presentation for this commutative monoid object. Using this presentation, one can quickly deduce Knudsen's formula for the rational cohomology of configuration spaces, prove rational homological stability and understand how automorphisms of the manifold act on the cohomology of configuration spaces. Similar considerations reproduce the work of Farb–Wolfson–Wood on homological densities.
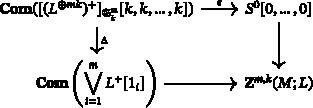
作为交换单体的配置空间
经过一点压缩后,流形的所有无序构型空间的集合可以通过构型叠加实现交换乘法。我们解释了这一交换一元对象的简单(派生)表述。利用这一表述,我们可以快速推导出配置空间的有理同调公式,证明有理同调稳定性,并理解流形的自动态如何作用于配置空间的同调。类似的考虑再现了法布-沃尔夫森-伍德关于同调密度的工作。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
1.90
自引率
0.00%
发文量
198
审稿时长
4-8 weeks
期刊介绍:
Published by Oxford University Press prior to January 2017: http://blms.oxfordjournals.org/

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


