Interpolation of fat points on K3 and abelian surfaces
IF 0.8
3区 数学
Q2 MATHEMATICS
引用次数: 0
Abstract
We prove that any number of general fat points of any multiplicities impose the expected number of conditions on a linear system on a smooth projective surface, in several cases including primitive linear systems on very general K3 and abelian surfaces, “Du Val” linear systems on blowups of at nine very general points, and certain linear systems on some ruled surfaces over elliptic curves. This is done by answering a question of the author about the case of only one fat point on a certain ruled surface, which follows from a circle of results due to Treibich–Verdier, Segal–Wilson, and others.
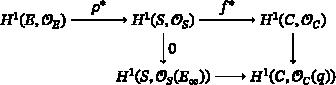
K3 和无常曲面上的胖点插值
我们证明,在光滑投影面上的线性系统上,任何倍数的一般胖点的数量都会对线性系统施加预期数量的条件,这些情况包括非常一般的 K3 和无差别面上的原始线性系统、P 2 ${\mathbb {P}}^2$ 的吹积上九个非常一般的点上的 "Du Val "线性系统,以及椭圆曲线上某些规则面上的某些线性系统。这是通过回答作者提出的一个问题来完成的,这个问题是关于在某个规则曲面上只有一个胖点的情况,而这个胖点是由 Treibich-Verdier、Segal-Wilson 等人的一圈结果得出的。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
1.90
自引率
0.00%
发文量
198
审稿时长
4-8 weeks
期刊介绍:
Published by Oxford University Press prior to January 2017: http://blms.oxfordjournals.org/

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


