Quantum-classical separations in shallow-circuit-based learning with and without noises
IF 5.4
1区 物理与天体物理
Q1 PHYSICS, MULTIDISCIPLINARY
引用次数: 0
Abstract
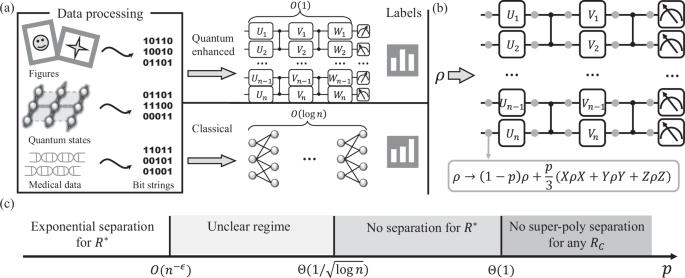
An essential problem in quantum machine learning is to find quantum-classical separations between learning models. However, rigorous and unconditional separations are lacking for supervised learning. Here we construct a classification problem defined by a noiseless constant depth (i.e., shallow) quantum circuit and rigorously prove that any classical neural network with bounded connectivity requires logarithmic depth to output correctly with a larger-than-exponentially-small probability. This unconditional near-optimal quantum-classical representation power separation originates from the quantum nonlocality property that distinguishes quantum circuits from their classical counterparts. We further characterize the noise regimes for demonstrating such a separation on near-term quantum devices under the depolarization noise model. In addition, for quantum devices with constant noise strength, we prove that no super-polynomial classical-quantum separation exists for any classification task defined by Clifford circuits, independent of the structures of the circuits that specify the learning models. An essential problem in quantum machine learning is to find quantum-classical separations between learning models. The authors construct a classification problem based on constant depth quantum circuit to rigorously prove that such a separation exists in terms of representation power, and further characterize the noise regimes for the separation to exist.
基于浅层电路的有噪声和无噪声学习中的量子经典分离
量子机器学习的一个基本问题是找到学习模型之间的量子经典分离。然而,监督学习缺乏严格的无条件分离。在这里,我们构建了一个由无噪声恒定深度(即浅)量子电路定义的分类问题,并严格证明了任何具有有界连接性的经典神经网络都需要对数深度才能以大于指数的小概率正确输出。这种无条件的近优量子-经典表示力分离源于量子非局域性特性,该特性将量子电路与经典电路区分开来。在去极化噪声模型下,我们进一步描述了在近期量子设备上证明这种分离的噪声环境。此外,对于具有恒定噪声强度的量子设备,我们证明,对于任何由克利福德电路定义的分类任务,都不存在超多项式经典-量子分离,这与指定学习模型的电路结构无关。量子机器学习的一个基本问题是找到学习模型之间的量子经典分离。作者构建了一个基于恒定深度量子电路的分类问题,从表征力的角度严格证明了这种分离的存在,并进一步描述了分离存在的噪声状态。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Communications Physics
Physics and Astronomy-General Physics and Astronomy
CiteScore
8.40
自引率
3.60%
发文量
276
审稿时长
13 weeks
期刊介绍:
Communications Physics is an open access journal from Nature Research publishing high-quality research, reviews and commentary in all areas of the physical sciences. Research papers published by the journal represent significant advances bringing new insight to a specialized area of research in physics. We also aim to provide a community forum for issues of importance to all physicists, regardless of sub-discipline.
The scope of the journal covers all areas of experimental, applied, fundamental, and interdisciplinary physical sciences. Primary research published in Communications Physics includes novel experimental results, new techniques or computational methods that may influence the work of others in the sub-discipline. We also consider submissions from adjacent research fields where the central advance of the study is of interest to physicists, for example material sciences, physical chemistry and technologies.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


