Bridging scales in multiscale bubble growth dynamics with correlated fluctuations using neural operator learning

Abstract

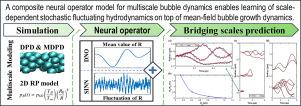
The intricate process of bubble growth dynamics involves a broad spectrum of physical phenomena from microscale mechanics of bubble formation to macroscale interplay between bubbles and surrounding thermo-hydrodynamics. Traditional bubble dynamics models including atomistic approaches and continuum-based methods segment the bubble dynamics into distinct scale-specific models. To bridge the gap between microscale stochastic fluid models and continuum-based fluid models for bubble dynamics, we develop a composite neural operator model to unify the analysis of nonlinear bubble dynamics across microscale and macroscale regimes by integrating a many-body dissipative particle dynamics (mDPD) model with a continuum-based Rayleigh–Plesset (RP) model through a novel neural network architecture, which consists of a deep operator network for learning the mean behavior of bubble growth subject to pressure variations and a long short-term memory network for learning the statistical features of correlated fluctuations in microscale bubble dynamics. Training and testing data are generated by conducting mDPD and RP simulations for nonlinear bubble dynamics with initial bubble radii ranging from 0.1 to 1.5 micrometers. The results show that the trained composite neural operator model can accurately predict bubble dynamics across scales, with a 99% predictive accuracy for the time evolution of the bubble radius under varying external pressure while containing correct size-dependent stochastic fluctuations in microscale bubble growth dynamics. The composite neural operator is the first deep learning surrogate for multiscale bubble growth dynamics that can capture correct stochastic fluctuations in microscopic fluid phenomena, which sets a new direction for future research in multiscale fluid dynamics modeling.