Data-driven continuum damage mechanics with built-in physics

Abstract

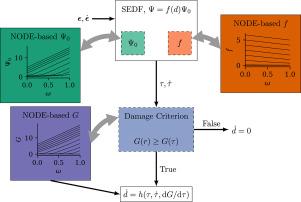
Soft materials such as rubbers and soft tissues often undergo large deformations and experience damage degradation that impairs their function. This energy dissipation mechanism can be described in a thermodynamically consistent framework known as continuum damage mechanics. Recently, data-driven methods have been developed to capture complex material behaviors with unmatched accuracy due to the high flexibility of deep learning architectures. Initial efforts focused on hyperelastic materials, and recent advances now offer the ability to satisfy physics constraints such as polyconvexity of the strain energy density function by default. However, modeling inelastic behavior with deep learning architectures and built-in physics has remained challenging. Here we show that neural ordinary differential equations (NODEs), which we used previously to model arbitrary hyperelastic materials with automatic polyconvexity, can be extended to model energy dissipation in a thermodynamically consistent way by introducing an inelastic potential: a monotonic yield function. We demonstrate the inherent flexibility of our network architecture in terms of different damage models proposed in the literature. Our results suggest that our NODEs re-discover the true damage function from synthetic stress-deformation history data. In addition, they can accurately characterize experimental skin and subcutaneous tissue data.