Fast partitioning of Pauli strings into commuting families for optimal expectation value measurements of dense operators
IF 2.9
2区 物理与天体物理
Q2 Physics and Astronomy
引用次数: 0
Abstract
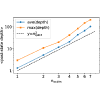
The Pauli strings appearing in the decomposition of an operator can be can be grouped into commuting families, reducing the number of quantum circuits needed to measure the expectation value of the operator. We detail an algorithm to completely partition the full set of Pauli strings acting on any number of qubits into the minimal number of sets of commuting families, and we provide python code to perform the partitioning. The partitioning method scales linearly with the size of the set of Pauli strings and it naturally provides a fast method of diagonalizing the commuting families with quantum gates. We provide a package that integrates the partitioning into qiskit, and use this to benchmark the algorithm with dense Hamiltonians, such as those that arise in matrix quantum mechanics models, on IBM hardware. We demonstrate computational speedups close to the theoretical limit of relative to qubit-wise commuting groupings, for qubits.
将保利弦快速划分为换向族,以实现密集算子的最佳期望值测量
在算子分解中出现的保利弦可以被归类为换向族,从而减少测量算子期望值所需的量子电路数量。我们详细介绍了将作用于任意数量量子比特的全套保利弦完全划分为最小数量换向族集合的算法,并提供了执行划分的 python 代码。分割方法与保利弦集的大小成线性比例,它自然提供了一种用量子门对角化换向族的快速方法。我们提供了一个软件包,将分割方法集成到 qiskit 中,并利用它在 IBM 硬件上对密集哈密顿(如矩阵量子力学模型中出现的哈密顿)进行基准测试。我们展示了在 m=2,...6 量子位时,相对于量子位换向分组,计算速度接近理论极限 (3/2)m。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Physical Review A
物理-光学
CiteScore
5.40
自引率
24.10%
发文量
0
审稿时长
2.2 months
期刊介绍:
Physical Review A (PRA) publishes important developments in the rapidly evolving areas of atomic, molecular, and optical (AMO) physics, quantum information, and related fundamental concepts.
PRA covers atomic, molecular, and optical physics, foundations of quantum mechanics, and quantum information, including:
-Fundamental concepts
-Quantum information
-Atomic and molecular structure and dynamics; high-precision measurement
-Atomic and molecular collisions and interactions
-Atomic and molecular processes in external fields, including interactions with strong fields and short pulses
-Matter waves and collective properties of cold atoms and molecules
-Quantum optics, physics of lasers, nonlinear optics, and classical optics
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


